Simple search vs Binary search
by Aditya Y. Bhargava This book is aimed at anyone who knows the basics of coding and wants to understand algorithms. Maybe you already have a coding problem and are trying to find an algorithmic solution. 1. Introduction to #algorithms In this chapter: You get a foundation for the rest of the book. You write your first search algorithm (binary search) You learn how to talk about the running time of an algorithm (Big O notation). You’re introduced to a common technique for designing algorithms (recursion). Binary search Binary search is an #algorithm; its input is a sorted list of elements. If an element you’re looking for is in that list, binary search returns the position where it’s located. Otherwise, binary search returns null. Simple search vs Binary search Simple search (maybe stupid search would be a better term). With each guess, you’re eliminating only one number. If my number was 99, it could take you 99 guesses to get there! With binary search, you guess the middle number and eliminate half the remaining numbers every time. Let me explain: Same case (0-100) Start with 50. Too low, but you just eliminated half the numbers! Now you know that 1–50 are all "too low" (You should skip all them) Next guess: 75. Too high, but again you cut down half the remaining numbers! (Skip 75 to 100) Next is 63 (halfway between 50 and 75). ... Suppose you’re looking for a word in the dictionary. The dictionary has 240,000 words. In the worst case, how many steps do you think each search will take? Simple search could take 240,000 steps. Binary search will take 18 steps. function binary_search(list: T[], item: T): number | null { let low: number = 0; let high: number = list.length - 1; while (low item) { high = mid - 1; } else { low = mid + 1; } } return null; } // Example usage: const numbers = [1, 3, 5, 7, 9, 11, 13, 15]; const target = 7; const result = binarySearch(numbers, target); console.log(result); // Output: 3 Exercise: Suppose you have a sorted list of 128 names, and you’re searching through it using binary search. What’s the maximum number of steps it would take? The maximum number of steps binary search takes can be determined using the formula: $$ log_2(n) $$ where nn is the number of elements in the list. In this case, n=128n = 128: $$ log_2(128) = 7 $$ So, the maximum number of steps it would take to find a name in a sorted list of 128 names using binary search is 7 steps.

by Aditya Y. Bhargava
This book is aimed at anyone who knows the basics of coding and wants to understand algorithms. Maybe you already have a coding problem and are trying to find an algorithmic solution.
1. Introduction to #algorithms
In this chapter:
- You get a foundation for the rest of the book.
- You write your first search algorithm (binary search)
- You learn how to talk about the running time of an algorithm (Big O notation).
- You’re introduced to a common technique for designing algorithms (recursion).
Binary search
Binary search is an #algorithm; its input is a sorted list of elements. If an element you’re looking for is in that list, binary search returns the position where it’s located.
Otherwise, binary search returns null.
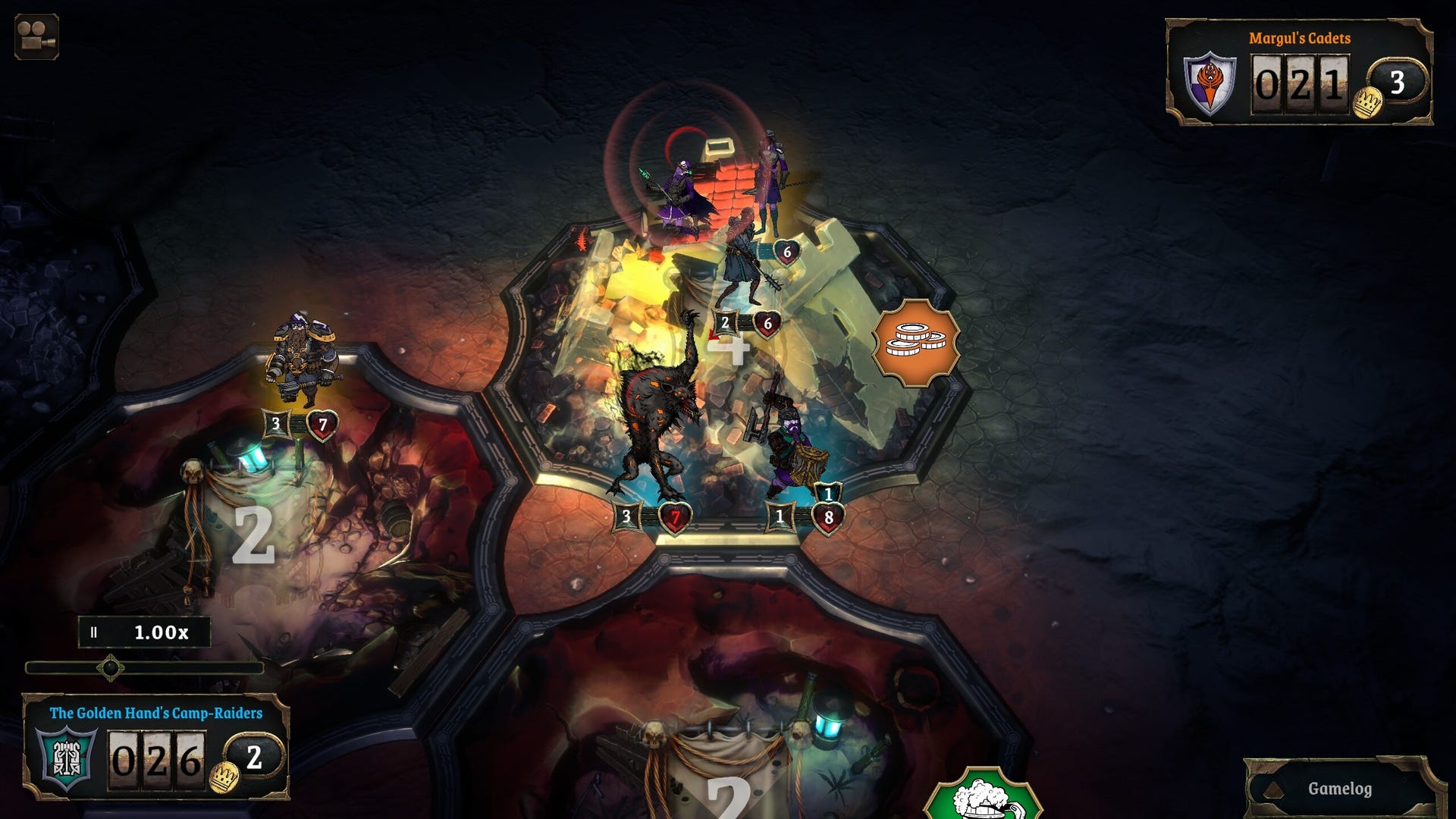
Simple search vs Binary search
Simple search (maybe stupid search would be a better term). With each guess, you’re eliminating only one number. If my number was 99, it could take you 99 guesses to get there!
With binary search, you guess the middle number and eliminate half the remaining numbers every time. Let me explain: Same case (0-100)
- Start with 50.
- Too low, but you just eliminated half the numbers!
- Now you know that 1–50 are all "too low" (You should skip all them)
- Next guess: 75.
- Too high, but again you cut down half the remaining numbers! (Skip 75 to 100)
- Next is 63 (halfway between 50 and 75).
- ...
Suppose you’re looking for a word in the dictionary. The dictionary has 240,000 words. In the worst case, how many steps do you think each search will take?
- Simple search could take 240,000 steps.
- Binary search will take 18 steps.
function binary_search<T>(list: T[], item: T): number | null {
let low: number = 0;
let high: number = list.length - 1;
while (low <= high) {
let mid: number = Math.floor((low + high) / 2);
let guess: T = list[mid];
if (guess === item) {
return mid;
}
if (guess > item) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return null;
}
// Example usage:
const numbers = [1, 3, 5, 7, 9, 11, 13, 15];
const target = 7;
const result = binarySearch(numbers, target);
console.log(result); // Output: 3
Exercise:
Suppose you have a sorted list of 128 names, and you’re searching through it using binary search.
What’s the maximum number of steps it would take?
The maximum number of steps binary search takes can be determined using the formula:
$$
log_2(n)
$$
where nn is the number of elements in the list. In this case, n=128n = 128:
$$
log_2(128) = 7
$$
So, the maximum number of steps it would take to find a name in a sorted list of 128 names using binary search is 7 steps.
































































![iFixit Tears Down New M4 MacBook Air [Video]](https://www.iclarified.com/images/news/96717/96717/96717-640.jpg)

![Apple Officially Announces Return of 'Ted Lasso' for Fourth Season [Video]](https://www.iclarified.com/images/news/96710/96710/96710-640.jpg)



























































































































































![[The AI Show Episode 139]: The Government Knows AGI Is Coming, Superintelligence Strategy, OpenAI’s $20,000 Per Month Agents & Top 100 Gen AI Apps](https://www.marketingaiinstitute.com/hubfs/ep%20139%20cover-2.png)


![[The AI Show Episode 138]: Introducing GPT-4.5, Claude 3.7 Sonnet, Alexa+, Deep Research Now in ChatGPT Plus & How AI Is Disrupting Writing](https://www.marketingaiinstitute.com/hubfs/ep%20138%20cover.png)






































































































![How to become a self-taught developer while supporting a family [Podcast #164]](https://cdn.hashnode.com/res/hashnode/image/upload/v1741989957776/7e938ad4-f691-4c9e-8c6b-dc26da7767e1.png?#)
































.jpg?#)

.jpg?#)