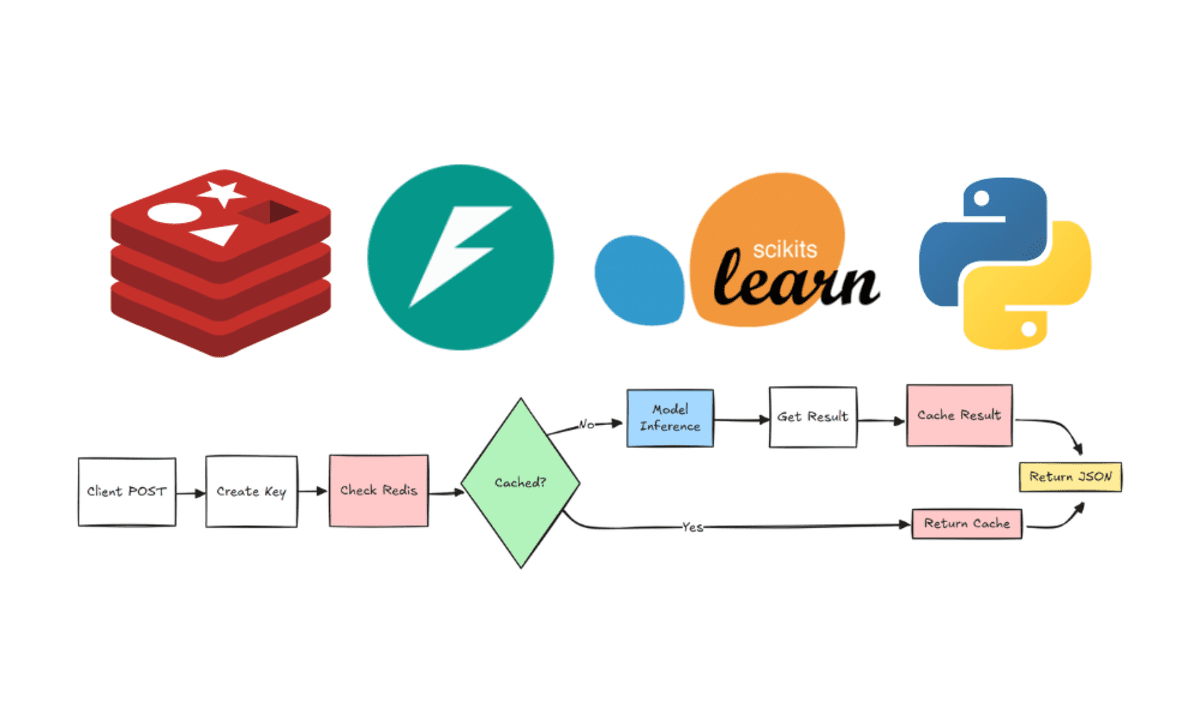
Verify LLMs: How to Spot Fake AI in Decentralized Networks
This is a Plain English Papers summary of a research paper called Verify LLMs: How to Spot Fake AI in Decentralized Networks. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter. The Challenge of Verifying LLMs in Decentralized Networks Decentralized AI networks like Gaia enable individuals to run customized large language models (LLMs) on personal computers and offer these services to the public. This decentralization brings numerous benefits: enhanced privacy, reduced costs, faster response times, and improved availability. More importantly, it fosters an ecosystem where AI services can be tailored with proprietary data and specialized knowledge. However, this freedom creates a significant challenge. Since these networks must remain permissionless to reduce censorship and maintain accessibility, nodes might claim to run one model while actually operating a different one. When popular model domains might host over 1,000 nodes simultaneously, the network requires a reliable mechanism to detect and penalize dishonest participants. This verification challenge is particularly difficult because traditional cryptographic methods often prove impractical at scale. The research presents a novel approach using statistical analysis of model outputs combined with cryptoeconomic incentives to ensure network integrity. Prior Approaches to LLM Verification: Why Cryptographic Methods Fall Short Researchers have previously explored deterministic verification through cryptographic algorithms, but these methods face significant limitations: Zero Knowledge Proofs (ZKP) theoretically allow verification of computation outcomes without knowing internal system details. However, ZKP for LLM verification faces several obstacles: Each ZKP circuit must be custom-generated for individual LLMs, requiring enormous engineering effort across thousands of models Even state-of-the-art ZKP algorithms need 13 minutes to generate proof for a single inference from a small 13B parameter model—100× slower than the inference itself Memory requirements are prohibitive—a toy LLM with one million parameters requires 25GB of RAM for proof generation Open-source LLMs remain vulnerable to proof forgery Trusted Execution Environments (TEE) embedded in CPUs and GPUs can generate signed attestations for software and data. However, TEE implementation faces its own challenges: Reduces raw CPU performance by up to 2×, unacceptable for already compute-bound LLM inference Very few GPUs or AI accelerators currently support TEEs Cannot verify that an LLM server is actually using the verified model for serving requests Distributing private keys to decentralized TEE devices requires specialized infrastructure Given these limitations, cryptoeconomic mechanisms offer a more promising approach. This method assumes most participants are honest and uses social consensus to identify dishonest actors. Through staking and slashing, the network incentivizes honest behavior and penalizes cheating, creating a virtuous cycle within the ecosystem. Statistical Detection Hypothesis: Using Answer Patterns to Identify Models The research hypothesizes that by analyzing question responses from Gaia nodes, statistical distributions can reveal outliers running different LLMs or knowledge bases than advertised. Specifically, when asking a question to all nodes in a domain, honest nodes' answers should form a tight cluster in high-dimensional embedding space. Outliers that fall far outside this cluster likely run different models or knowledge bases than required. The mathematical approach involves: Sending questions (q) from set Q to nodes (m) from set M Repeating each question n times per node to create answer distributions Converting each answer to a z-dimensional vector (embedding) representing its semantic meaning Calculating mean points and distances between answer clusters Measuring consistency within a node's answers via standard deviation This framework allows for quantitative comparison between nodes, revealing statistical patterns that can distinguish between different models and knowledge bases. Experimental Design: Testing Model and Knowledge Base Detection The researchers conducted two key experiments to validate their hypothesis: First Experiment: Distinguishing Between LLM Models Three Gaia nodes were set up with different open-source LLMs: Llama 3.1 8b by Meta AI Gemma 2 9b by Google Gemma 2 27b by Google Each model was queried with 20 factual questions covering science, history, and geography, with each question repeated 25 times per model. This generated 500 responses per model and 1,500 responses total. Second Experiment: Distinguishing Between Knowledge Bases Two Gaia nodes were configured with identical LLMs (Gemma-2-9b) but different vector databases: One containing knowledge about Paris One containing knowledge about London Each kno
This is a Plain English Papers summary of a research paper called Verify LLMs: How to Spot Fake AI in Decentralized Networks. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.
The Challenge of Verifying LLMs in Decentralized Networks
Decentralized AI networks like Gaia enable individuals to run customized large language models (LLMs) on personal computers and offer these services to the public. This decentralization brings numerous benefits: enhanced privacy, reduced costs, faster response times, and improved availability. More importantly, it fosters an ecosystem where AI services can be tailored with proprietary data and specialized knowledge.
However, this freedom creates a significant challenge. Since these networks must remain permissionless to reduce censorship and maintain accessibility, nodes might claim to run one model while actually operating a different one. When popular model domains might host over 1,000 nodes simultaneously, the network requires a reliable mechanism to detect and penalize dishonest participants.
This verification challenge is particularly difficult because traditional cryptographic methods often prove impractical at scale. The research presents a novel approach using statistical analysis of model outputs combined with cryptoeconomic incentives to ensure network integrity.
Prior Approaches to LLM Verification: Why Cryptographic Methods Fall Short
Researchers have previously explored deterministic verification through cryptographic algorithms, but these methods face significant limitations:
Zero Knowledge Proofs (ZKP) theoretically allow verification of computation outcomes without knowing internal system details. However, ZKP for LLM verification faces several obstacles:
- Each ZKP circuit must be custom-generated for individual LLMs, requiring enormous engineering effort across thousands of models
- Even state-of-the-art ZKP algorithms need 13 minutes to generate proof for a single inference from a small 13B parameter model—100× slower than the inference itself
- Memory requirements are prohibitive—a toy LLM with one million parameters requires 25GB of RAM for proof generation
- Open-source LLMs remain vulnerable to proof forgery
Trusted Execution Environments (TEE) embedded in CPUs and GPUs can generate signed attestations for software and data. However, TEE implementation faces its own challenges:
- Reduces raw CPU performance by up to 2×, unacceptable for already compute-bound LLM inference
- Very few GPUs or AI accelerators currently support TEEs
- Cannot verify that an LLM server is actually using the verified model for serving requests
- Distributing private keys to decentralized TEE devices requires specialized infrastructure
Given these limitations, cryptoeconomic mechanisms offer a more promising approach. This method assumes most participants are honest and uses social consensus to identify dishonest actors. Through staking and slashing, the network incentivizes honest behavior and penalizes cheating, creating a virtuous cycle within the ecosystem.
Statistical Detection Hypothesis: Using Answer Patterns to Identify Models
The research hypothesizes that by analyzing question responses from Gaia nodes, statistical distributions can reveal outliers running different LLMs or knowledge bases than advertised.
Specifically, when asking a question to all nodes in a domain, honest nodes' answers should form a tight cluster in high-dimensional embedding space. Outliers that fall far outside this cluster likely run different models or knowledge bases than required.
The mathematical approach involves:
- Sending questions (q) from set Q to nodes (m) from set M
- Repeating each question n times per node to create answer distributions
- Converting each answer to a z-dimensional vector (embedding) representing its semantic meaning
- Calculating mean points and distances between answer clusters
- Measuring consistency within a node's answers via standard deviation
This framework allows for quantitative comparison between nodes, revealing statistical patterns that can distinguish between different models and knowledge bases.
Experimental Design: Testing Model and Knowledge Base Detection
The researchers conducted two key experiments to validate their hypothesis:
First Experiment: Distinguishing Between LLM Models
Three Gaia nodes were set up with different open-source LLMs:
- Llama 3.1 8b by Meta AI
- Gemma 2 9b by Google
- Gemma 2 27b by Google
Each model was queried with 20 factual questions covering science, history, and geography, with each question repeated 25 times per model. This generated 500 responses per model and 1,500 responses total.
Second Experiment: Distinguishing Between Knowledge Bases
Two Gaia nodes were configured with identical LLMs (Gemma-2-9b) but different vector databases:
- One containing knowledge about Paris
- One containing knowledge about London
Each knowledge base was queried with 20 factual questions evenly covering Paris and London topics, with each question repeated 25 times. This generated 500 responses per knowledge base and 1,000 responses total.
For all responses, a standard system prompt ("You are a helpful assistant") was used, and embeddings were generated using the gte-Qwen2-1.5B-instruct model for analysis.
How Different LLMs Have Distinct Response Patterns
The first experiment revealed clear statistical differences between LLM outputs:

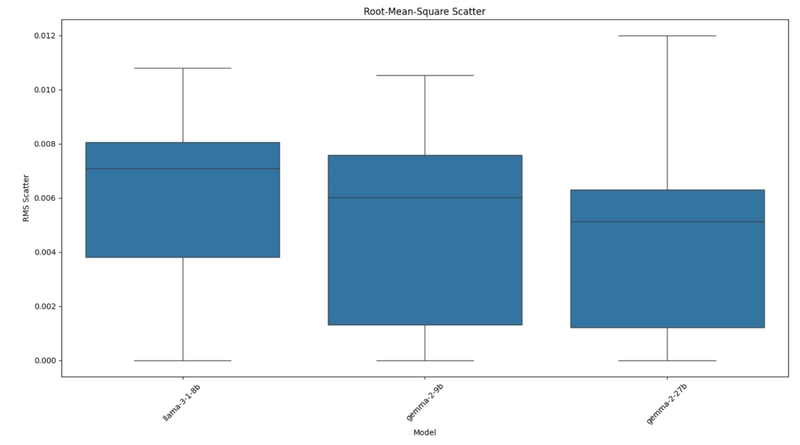
Figure 1: Internal consistency of different LLMs measured by RMS scatter.
The consistency metrics showed Gemma-2-27b demonstrating the highest consistency in responses with an RMS scatter of 0.0043, while Llama-3.1-8b showed the highest variation with an RMS scatter of 0.0062.
When comparing answers between models, substantial differences emerged:
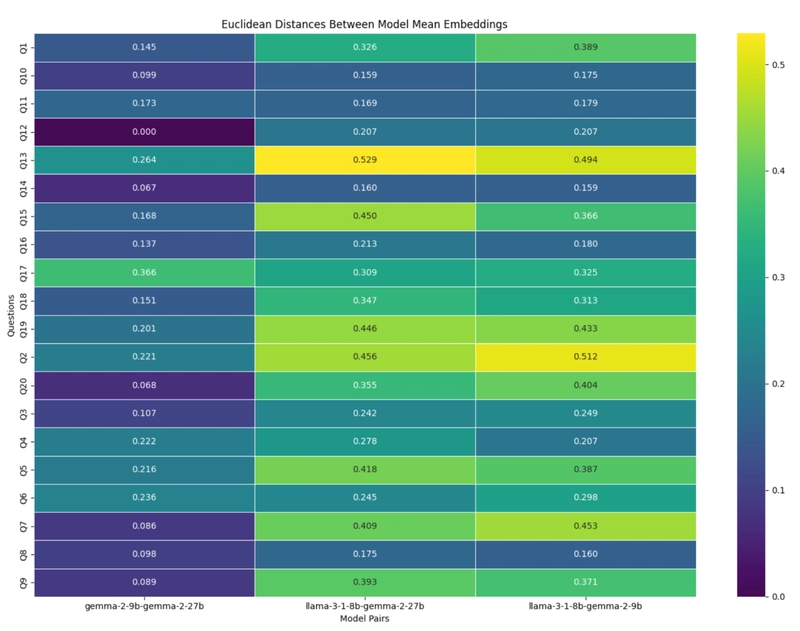
Figure 2: Average distance vs RMS scatter for each question and model pair.
The distances between model pairs varied by question, with the highest distance (0.5291) observed between Llama-3.1-8b and Gemma-2-27b for the question "Who wrote 'Romeo and Juliet'?" and the lowest non-zero distance (0.0669) between Gemma models for "What is the atomic number of oxygen?"
Most importantly, the data showed that distances between model pairs were dramatically larger than variations within any single model:
| Model pair | $D_{\text {ave }}$ | $D_{\text {ave }} / \sigma_{\text {max }}$ |
|---|---|---|
| Gemma9b - Gemma27b | 0.1558 | $32.5 \times$ |
| Llama8b - Gemma9b | 0.3129 | $65.2 \times$ |
| Llama8b - Gemma27b | 0.3141 | $65.4 \times$ |
Table 1: Average distance over max RMS scatter for each pair of LLMs
This 32-65× separation between inter-model distances and intra-model variation demonstrates that different LLMs produce reliably distinguishable outputs, making them identifiable through statistical analysis of their responses.
Knowledge Bases Leave Distinct Fingerprints in LLM Outputs
The second experiment showed that even with identical LLMs, different knowledge bases create statistically distinguishable response patterns:
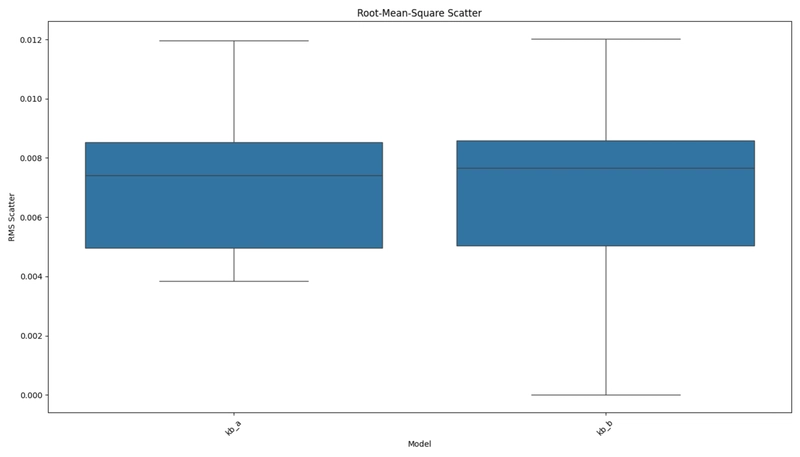
Figure 3: Internal consistency of different knowledge bases measured by RMS scatter.
The consistency metrics indicated that both knowledge bases generated responses with similar internal consistency. However, when comparing responses between knowledge bases, clear differences emerged:
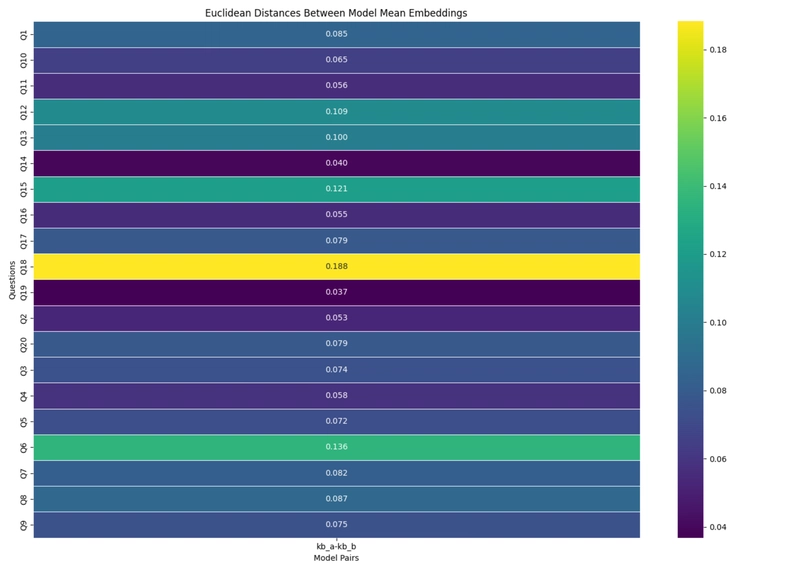
Figure 4: Average distance vs RMS scatter for each question and knowledge base pair.
The highest distance observed was 0.188 between Paris and London knowledge bases for the question "How many bridges did Philip Augustus build in Paris in the late 12th century?" The lowest non-zero distance was 0.037 for the question "What percentage of Paris's salaried employees work in hotels and restaurants according to the document?"
Critically, the distances between knowledge base pairs (average 0.0862) were 5-26× larger than variations within any knowledge base (0.0072). This significant separation indicates that nodes with different knowledge bases produce reliably distinguishable outputs, allowing for effective verification through statistical analysis.
Important Considerations: Factors Affecting Model Identification
Several important factors influence the effectiveness of statistical verification:
Family resemblance: Models from the same family (like the two Gemma models) show more similarity (distance of 0.1558) than models from different families (distances around 0.31). While still 32× greater than internal variations, this suggests distinguishing between models within the same family presents different challenges than cross-family comparisons.
Knowledge base similarities: Different knowledge bases produce more similar answers (distances around 0.1) than different LLM models, possibly because both test knowledge bases covered European capitals. Despite semantic similarities, the statistical differences remain sufficient for reliable detection.
Question effectiveness: Different questions demonstrated varying levels of differentiation. For example, "Who wrote 'Romeo and Juliet'?" showed the greatest distance between models (0.5291), while "How many bridges did Philip Augustus build in Paris in the late 12th century?" most effectively distinguished between knowledge bases (0.188). This variation highlights the importance of careful question selection in practical verification systems.
Further research is needed to determine how hardware variations, load conditions, and model updates might affect verification reliability.
Implementing Verification in a Decentralized Network: The AVS Design
Based on these findings, the researchers propose an Active Verification System (AVS) for the Gaia network:
Operator Sets Structure:
- Set 0: AVS validators responsible for polling nodes and detecting outliers (approved by Gaia DAO)
- Sets 1-n: Mapped to Gaia domains, with all nodes in each domain forming a single operator set
Verification Process:
- Each verification epoch lasts 12 hours
- Validators poll nodes with random questions from domain-specific question sets
- All responses, timeouts, and error messages are recorded
- Outlier detection is performed on responses
- Results are time-encrypted, signed, and posted on EigenDA
Node Flagging System:
- outlier: Node produces statistical outliers compared to other nodes
- slow: Node responds significantly slower than domain average
- timeout: Node timed out on one or more requests
- error 500: Node returned internal server errors
- error 404: Node returned resource unavailability errors
- error other: Node returned other HTTP error codes
Rewards and Penalties:
- Nodes maintaining good status across epochs receive regular AVS rewards
- Flagged nodes may be suspended from rewards and domain participation
- Malicious actors may have their stakes slashed
The AVS can also automate node onboarding by verifying that candidate nodes meet domain requirements for LLM, knowledge base, and response speed.
Conclusions: Making Decentralized AI Networks Trustworthy Through Statistical Verification
The research demonstrates that statistical analysis of LLM outputs can reliably identify the underlying model and knowledge base. This approach enables decentralized AI networks to use EigenLayer AVS to verify LLM outputs intersubjectively and detect outliers as potential bad actors.
By combining statistical verification with cryptoeconomic incentives and penalties, this method offers a practical solution for maintaining quality and trust in decentralized AI networks without requiring expensive cryptographic proofs or specialized hardware. The approach is particularly valuable because it scales effectively to large networks, making widespread decentralized AI inference more viable.
This verification framework represents a significant step toward building trustworthy decentralized AI systems that can deliver the benefits of local inference—privacy, cost-effectiveness, speed, and availability—while ensuring that users receive the specific model capabilities they expect.






































































![Apple Drops New Immersive Adventure Episode for Vision Pro: 'Hill Climb' [Video]](https://www.iclarified.com/images/news/97133/97133/97133-640.jpg)

![Most iPhones Sold in the U.S. Will Be Made in India by 2026 [Report]](https://www.iclarified.com/images/news/97130/97130/97130-640.jpg)









![This new Google TV streaming dongle looks just like a Chromecast [Gallery]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2025/04/thomson-cast-150-google-tv-1.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)


![Hostinger Horizons lets you effortlessly turn ideas into web apps without coding [10% off]](https://i0.wp.com/9to5mac.com/wp-content/uploads/sites/6/2025/04/IMG_1551.png?resize=1200%2C628&quality=82&strip=all&ssl=1)






















































































_Olekcii_Mach_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)
















































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)






























































































































































![[FREE EBOOKS] AI and Business Rule Engines for Excel Power Users, Machine Learning Hero & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)























































































.jpg?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)