Вертикальный обход бинарного дерева. 314. Binary Tree Vertical Order Traversal.
Задача Дано бинарное дерево. Нужно обойти дерево вертикально. Т.е. столбец за столбцом. В рамках одного столбца элементы должны быть сверху вниз. Для элементов, которые в одном столбце и одной строке, в результате они должны быть слева направо. Ссылка на leetcode: https://leetcode.com/problems/binary-tree-vertical-order-traversal Например, И случай, когда есть элементы 0 и 1, которые на одной строке и в одном столбце: Решение Почти все задачи на деревья - это задачи на применение DFS или BFS. В данном случае можно применить BFS и обходить дерево по слоям. При обходе дерева нам нужно знать номер столбца, в котором находится текущий элемент. Например, Элемент 9 в столбце 0, элементы 3 и 15 в столбце 1, элемент 20 в столбце 2, элемент 7 в столбце 3. Как вычислить номер столбца для текущего элемента? Например, можно указать номером столбца корня дерева - 0. Тогда для левого ребенка номер столбца будет на единицу меньше, чем у родительской вершины - column - 1, а для правого на единицу больше column + 1. Аналогично, для оставшихся вершин: Таким образов, обходя дерево, мы знаем его текущий столбец. Зная столбец текущего элемента мы можем сохранить результат в хэш-таблице. Где ключ - это номер столбца, а значение - список элементов в этом столбце. Т.к. нам нужно вернуть результат в виде списка списков, необходимо перенормировать номера столбцов. Иначе при таком подходе они могут оказаться отрицательными. Чтобы этого избежать, при обходе дерева будем отслеживать минимальный и максимальный номера столбцов, а затем использовать их для финальной трансформации хеш-таблицы. Реализация Напишем вначале базовый обход дерева при помощи BFS: public List verticalOrder(TreeNode root) { if (root == null) { return new ArrayList(); } Queue queue = new ArrayDeque(); queue.offer(root); while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } List result = new ArrayList(); return result; } Добавим вычисление текущего столбца (для левого ребенка column - 1, для правого column + 1). Номера столбцов можно поместить в туже очередь queue, но придется помещать пары: вершина и номер столбца. Также можно в отдельную очередь: public List verticalOrder(TreeNode root) { if (root == null) { return new ArrayList(); } Queue queue = new ArrayDeque(); //Очередь, где храним столбец соответствующей вершины из queue Queue columnsQueue = new ArrayDeque(); queue.offer(root); columnsQueue.offer(0); while (!queue.isEmpty()) { TreeNode node = queue.poll(); Integer column = columnsQueue.poll(); if (node.left != null) { queue.offer(node.left); columnsQueue.offer(column - 1); } if (node.right != null) { queue.offer(node.right); columnsQueue.offer(column + 1); } } List result = new ArrayList(); return result; } Добавим сохранение результата в HashMap, где ключ - это номер столбца, а значение это список вершин: public List verticalOrder(TreeNode root) { if (root == null) { return new ArrayList(); } Queue queue = new ArrayDeque(); Queue columnsQueue = new ArrayDeque(); queue.offer(root); columnsQueue.offer(0); Map map = new HashMap(); while (!queue.isEmpty()) { TreeNode node = queue.poll(); Integer column = columnsQueue.poll(); if (!map.containsKey(column)) { map.put(column, new ArrayList()); } map.get(column).add(node.val); if (node.left != null) { queue.offer(node.left); columnsQueue.offer(column - 1); } if (node.right != null) { queue.offer(node.right); columnsQueue.offer(column + 1); } } List result = new ArrayList(); return result; } И наконец добавим трекинг максимального и минимального столбца и финальную трансформацию HashMap в список списков: public List verticalOrder(TreeNode root) { if (root == null) { return new ArrayList(); } Queue queue = new ArrayDeque(); Queue columnsQueue = new ArrayDeque(); queue.offer(root); columnsQueue.offer(0); int minColumn = Integer.MAX_VALUE; int maxColumn = Integer.MIN_VALUE; Map map = new HashMap(); while (!queue.isEmpty()) { TreeNode node = queue.poll(); Integer column = columnsQueue.poll(); if (!map.containsKey(column)) { map.put(column, new ArrayList()); } map.get(column).add(node.val); minColumn = Math.min(minColumn, column); maxColumn = Math.max(maxColumn, column); if (node.left != null) { queue.offer(node.left); c
Задача
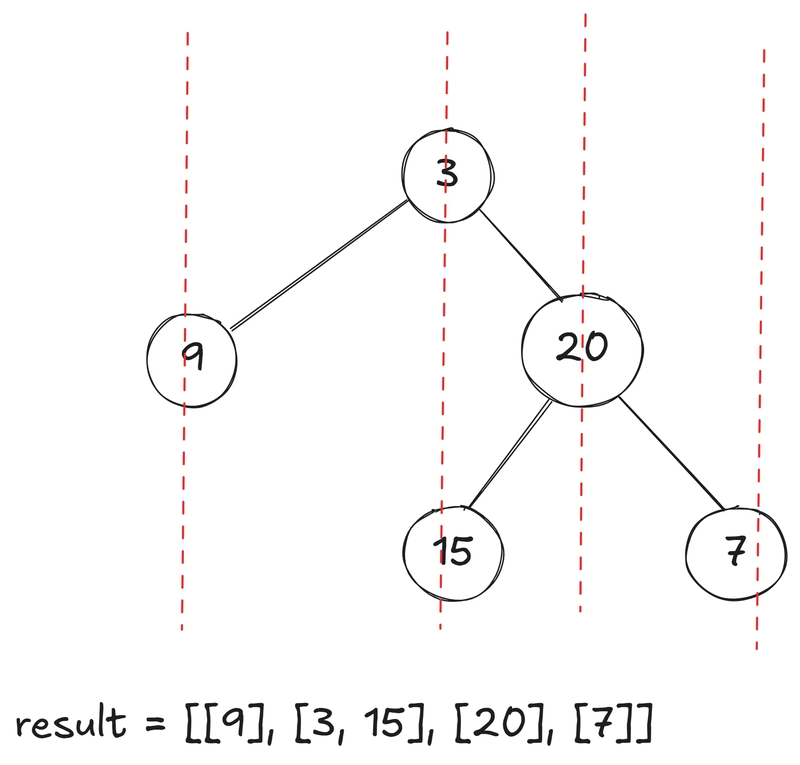
Дано бинарное дерево. Нужно обойти дерево вертикально. Т.е. столбец за столбцом. В рамках одного столбца элементы должны быть сверху вниз.
Для элементов, которые в одном столбце и одной строке, в результате они должны быть слева направо.
Ссылка на leetcode: https://leetcode.com/problems/binary-tree-vertical-order-traversal
Например,
И случай, когда есть элементы 0 и 1, которые на одной строке и в одном столбце:
Решение
Почти все задачи на деревья - это задачи на применение DFS или BFS. В данном случае можно применить BFS и обходить дерево по слоям.
При обходе дерева нам нужно знать номер столбца, в котором находится текущий элемент.
Например,
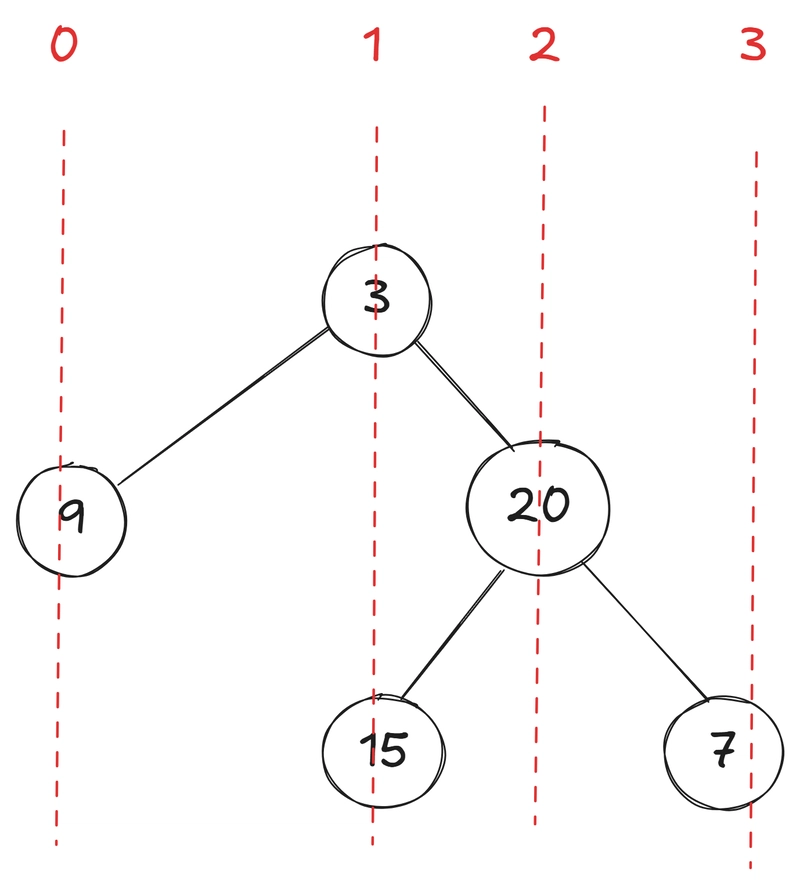
Элемент 9 в столбце 0, элементы 3 и 15 в столбце 1, элемент 20 в столбце 2, элемент 7 в столбце 3.
Как вычислить номер столбца для текущего элемента?
Например, можно указать номером столбца корня дерева - 0.
Тогда для левого ребенка номер столбца будет на единицу меньше, чем у родительской вершины - column - 1, а для правого на единицу больше column + 1.
Аналогично, для оставшихся вершин:
Таким образов, обходя дерево, мы знаем его текущий столбец. Зная столбец текущего элемента мы можем сохранить результат в хэш-таблице. Где ключ - это номер столбца, а значение - список элементов в этом столбце.
Т.к. нам нужно вернуть результат в виде списка списков, необходимо перенормировать номера столбцов. Иначе при таком подходе они могут оказаться отрицательными. Чтобы этого избежать, при обходе дерева будем отслеживать минимальный и максимальный номера столбцов, а затем использовать их для финальной трансформации хеш-таблицы.
Реализация
Напишем вначале базовый обход дерева при помощи BFS:
public List<List<Integer>> verticalOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
List<List<Integer>> result = new ArrayList<>();
return result;
}
Добавим вычисление текущего столбца (для левого ребенка column - 1, для правого column + 1). Номера столбцов можно поместить в туже очередь queue, но придется помещать пары: вершина и номер столбца. Также можно в отдельную очередь:
public List<List<Integer>> verticalOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
Queue<TreeNode> queue = new ArrayDeque<>();
//Очередь, где храним столбец соответствующей вершины из queue
Queue<Integer> columnsQueue = new ArrayDeque<>();
queue.offer(root);
columnsQueue.offer(0);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
Integer column = columnsQueue.poll();
if (node.left != null) {
queue.offer(node.left);
columnsQueue.offer(column - 1);
}
if (node.right != null) {
queue.offer(node.right);
columnsQueue.offer(column + 1);
}
}
List<List<Integer>> result = new ArrayList<>();
return result;
}
Добавим сохранение результата в HashMap, где ключ - это номер столбца, а значение это список вершин:
public List<List<Integer>> verticalOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
Queue<TreeNode> queue = new ArrayDeque<>();
Queue<Integer> columnsQueue = new ArrayDeque<>();
queue.offer(root);
columnsQueue.offer(0);
Map<Integer, List<Integer>> map = new HashMap<>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
Integer column = columnsQueue.poll();
if (!map.containsKey(column)) {
map.put(column, new ArrayList<>());
}
map.get(column).add(node.val);
if (node.left != null) {
queue.offer(node.left);
columnsQueue.offer(column - 1);
}
if (node.right != null) {
queue.offer(node.right);
columnsQueue.offer(column + 1);
}
}
List<List<Integer>> result = new ArrayList<>();
return result;
}
И наконец добавим трекинг максимального и минимального столбца и финальную трансформацию HashMap в список списков:
public List<List<Integer>> verticalOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
Queue<TreeNode> queue = new ArrayDeque<>();
Queue<Integer> columnsQueue = new ArrayDeque<>();
queue.offer(root);
columnsQueue.offer(0);
int minColumn = Integer.MAX_VALUE;
int maxColumn = Integer.MIN_VALUE;
Map<Integer, List<Integer>> map = new HashMap<>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
Integer column = columnsQueue.poll();
if (!map.containsKey(column)) {
map.put(column, new ArrayList<>());
}
map.get(column).add(node.val);
minColumn = Math.min(minColumn, column);
maxColumn = Math.max(maxColumn, column);
if (node.left != null) {
queue.offer(node.left);
columnsQueue.offer(column - 1);
}
if (node.right != null) {
queue.offer(node.right);
columnsQueue.offer(column + 1);
}
}
List<List<Integer>> result = new ArrayList<>();
for (int i = minColumn; i <= maxColumn; i++) {
result.add(map.get(i));
}
return result;
}
Time Complexity - O(N), где N - число вершин в дереве, т.к. мы обходим все вершины в дереве по одному разу.
Space Complexity - O(N), т.к. мы используем дополнительно HashMap, а также Queue для BFS.




























![Epic Games Wins Major Victory as Apple is Ordered to Comply With App Store Anti-Steering Injunction [Updated]](https://images.macrumors.com/t/Z4nU2dRocDnr4NPvf-sGNedmPGA=/2250x/article-new/2022/01/iOS-App-Store-General-Feature-JoeBlue.jpg)

























































![Google Home app fixes bug that repeatedly asked to ‘Set up Nest Cam features’ for Nest Hub Max [U]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2022/08/youtube-premium-music-nest-hub-max.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)















































































































































































































![[The AI Show Episode 145]: OpenAI Releases o3 and o4-mini, AI Is Causing “Quiet Layoffs,” Executive Order on Youth AI Education & GPT-4o’s Controversial Update](https://www.marketingaiinstitute.com/hubfs/ep%20145%20cover.png)



































































































![[DEALS] Mail Backup X Individual Edition: Lifetime Subscription (72% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)




































































.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)

.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)