Neural SDFs from Point Clouds: Heat Method for Accurate 3D Reconstruction

This is a Plain English Papers summary of a research paper called Neural SDFs from Point Clouds: Heat Method for Accurate 3D Reconstruction. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter. Introduction: A New Approach to Neural Signed Distance Fields Neural Signed Distance Fields (SDFs) have gained popularity for representing 3D surfaces due to their flexibility and performance in applications like shape reconstruction. While many volumetric functions can represent surfaces, SDFs are preferred for additional applications such as constructive solid geometry and collision detection. They also enable the use of level set methods for solving PDEs, which have numerous applications but have only recently been explored in neural settings. Creating an effective neural SDF requires meeting several criteria: accurate surface representation, precise non-zero level sets in a narrow band near the surface for differential computations, and the ability to be constructed directly from unoriented point clouds. Existing approaches often require approximated ground truth distances or learned priors, or they represent the zero-level set well but lack accuracy in the narrow band. The fundamental challenge lies in solving the eikonal equation (requiring the gradient of the SDF to have unit norm), which is difficult because it has many solutions. Only the viscosity solution corresponds to the true SDF, but neural networks optimized with gradient descent may converge to non-SDF local minima. Figure 1: Visualization of the two-step process: from point cloud to heat flow to neural SDF. This paper introduces a novel approach that replaces the eikonal equation with the heat method, a technique long used for computing distances on discrete surfaces but now adapted to the neural domain. The method defines two well-posed variational problems that can be effectively optimized with stochastic gradient descent using standard network architectures. The heat method offers significant advantages because it avoids the challenges of the eikonal equation by solving two well-posed elliptic PDEs instead. The approach first solves for a time step of heat flow and computes the gradient of the unsigned distance function. Then, it fits the computed gradients to obtain the signed distance, considering that the input point cloud is unoriented. Figure 2: Visualization of the method's stages from point cloud to heat flow to SDF isosurfaces. Compared to state-of-the-art methods, this approach (called HeatSDF) achieves a good balance between the fidelity of the zero-level set to the surface and the accuracy of the SDF in a narrow band. It works well on point clouds with non-uniform density and provides mathematical guarantees through proven existence of solutions for both steps. The key contributions include: A theoretically sound variational scheme to approximate the field of level set normals and then the signed distance Accurate neural SDFs for spatially varying point cloud densities State-of-the-art surface reconstruction and accurate recovery of SDF gradients Application to neural PDE solving on level sets Method: A Two-Step Approach to Computing Neural SDFs The method considers a surface

Apr 19, 2025 - 17:51

This is a Plain English Papers summary of a research paper called Neural SDFs from Point Clouds: Heat Method for Accurate 3D Reconstruction. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.

Introduction: A New Approach to Neural Signed Distance Fields

Neural Signed Distance Fields (SDFs) have gained popularity for representing 3D surfaces due to their flexibility and performance in applications like shape reconstruction. While many volumetric functions can represent surfaces, SDFs are preferred for additional applications such as constructive solid geometry and collision detection. They also enable the use of level set methods for solving PDEs, which have numerous applications but have only recently been explored in neural settings.

Creating an effective neural SDF requires meeting several criteria: accurate surface representation, precise non-zero level sets in a narrow band near the surface for differential computations, and the ability to be constructed directly from unoriented point clouds. Existing approaches often require approximated ground truth distances or learned priors, or they represent the zero-level set well but lack accuracy in the narrow band.

The fundamental challenge lies in solving the eikonal equation (requiring the gradient of the SDF to have unit norm), which is difficult because it has many solutions. Only the viscosity solution corresponds to the true SDF, but neural networks optimized with gradient descent may converge to non-SDF local minima.

Figure 1: Visualization of the two-step process: from point cloud to heat flow to neural SDF.

This paper introduces a novel approach that replaces the eikonal equation with the heat method, a technique long used for computing distances on discrete surfaces but now adapted to the neural domain. The method defines two well-posed variational problems that can be effectively optimized with stochastic gradient descent using standard network architectures.

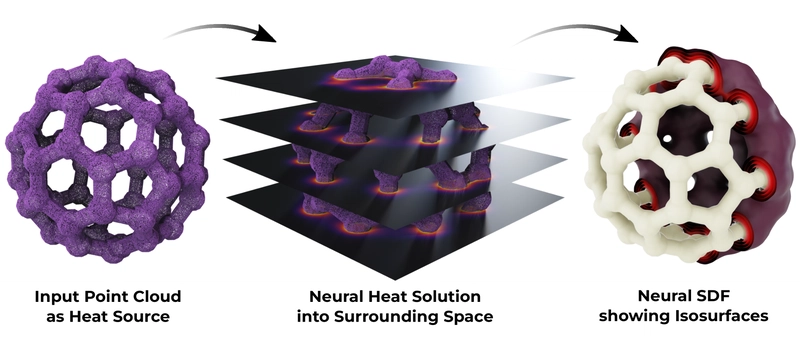
The heat method offers significant advantages because it avoids the challenges of the eikonal equation by solving two well-posed elliptic PDEs instead. The approach first solves for a time step of heat flow and computes the gradient of the unsigned distance function. Then, it fits the computed gradients to obtain the signed distance, considering that the input point cloud is unoriented.

Figure 2: Visualization of the method's stages from point cloud to heat flow to SDF isosurfaces.

Compared to state-of-the-art methods, this approach (called HeatSDF) achieves a good balance between the fidelity of the zero-level set to the surface and the accuracy of the SDF in a narrow band. It works well on point clouds with non-uniform density and provides mathematical guarantees through proven existence of solutions for both steps.

The key contributions include:

A theoretically sound variational scheme to approximate the field of level set normals and then the signed distance
Accurate neural SDFs for spatially varying point cloud densities
State-of-the-art surface reconstruction and accurate recovery of SDF gradients
Application to neural PDE solving on level sets

Method: A Two-Step Approach to Computing Neural SDFs

The method considers a surface