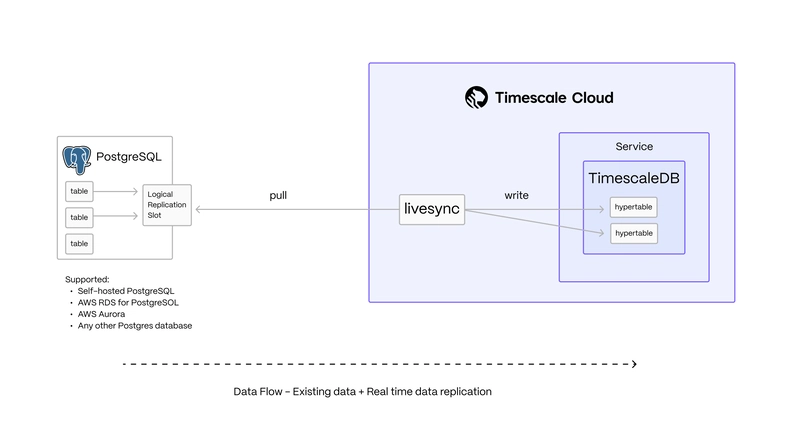
Efficient Edge Dominating Set Approximation for Sparse Graphs

Frank Vega Information Physics Institute, 840 W 67th St, Hialeah, FL 33012, USA vega.frank@gmail.com Problem Statement Given an undirected graph G=(V,E)G = (V, E)G=(V,E) , an edge dominating set is a subset of edges S⊆ES \subseteq ES⊆E such that every edge in EEE is either in SSS or shares at least one endpoint with an edge in SSS . Formally, for every edge (u,v)∈E(u, v) \in E(u,v)∈E , either (u,v)∈S(u, v) \in S(u,v)∈S , or there exists an edge (x,y)∈S(x, y) \in S(x,y)∈S such that (u,v)(u, v)(u,v) and (x,y)(x, y)(x,y) are adjacent (i.e., they share a common vertex). The goal of the Edge Dominating Set Problem is to find an edge dominating set SSS of minimum size. This problem is NP-hard, and the find_edge_dominating algorithm provides an approximate solution by transforming the problem into a dominating set problem on a line graph. Input: An undirected graph G=(V,E)G = (V, E)G=(V,E) , represented as a NetworkX graph. Output: A subset S⊆ES \subseteq ES⊆E such that every edge in EEE is either in SSS or adjacent to an edge in SSS , with ∣S∣|S|∣S∣ as small as possible. Algorithm Overview: find_edge_dominating The find_edge_dominating(graph) algorithm computes an approximate minimum edge dominating set by transforming the edge dominating set problem into a dominating set problem on the line graph of each connected component of the input graph. Consider the algorithm implemented in Python: import networkx as nx import baldor.algorithm as alg def find_edge_dominating(graph): """ Compute an approximate minimum edge dominating set set for an undirected graph by transforming it into a chordal graph. Args: graph (nx.Graph): A NetworkX Graph object representing the input graph. Returns: set: A set of vertex indices representing the minimum edge dominating set set. Returns an empty set if the graph is empty or has no edges. """ # Check if the input graph is a valid undirected NetworkX Graph; raises an error if not. if not isinstance(graph, nx.Graph): raise ValueError("Input must be an undirected NetworkX Graph.") # Handle edge cases: return an empty set if the graph has no nodes or no edges, as no edge dominating set is needed. if graph.number_of_nodes() == 0 or graph.number_of_edges() == 0: return set() # Remove all self-loop edges since they cannot be part of an edge dominating set. graph.remove_edges_from(list(nx.selfloop_edges(graph))) # Remove isolated nodes from the graph to process the remaining components, as they do not contribute to an edge dominating set. graph.remove_nodes_from(list(nx.isolates(graph))) # After removing isolated nodes, if the graph is empty, return an empty set (no edge dominating set needed). if graph.number_of_nodes() == 0: return set() # Initialize an empty set to store the approximate edge dominating set. approximate_edge_dominating = set() # Iterate over each connected component of the graph to compute the edge dominating set independently. for component in nx.connected_components(graph): # Extract the subgraph corresponding to the current connected component. subgraph = graph.subgraph(component) # Handle small components: if the subgraph has 2 or fewer edges, select one edge to dominate all edges in the component. if subgraph.number_of_edges()

Apr 28, 2025 - 23:49

Efficient Edge Dominating Set Approximation for Sparse Graphs

Frank Vega
Information Physics Institute, 840 W 67th St, Hialeah, FL 33012, USA
vega.frank@gmail.com

Problem Statement

Given an undirected graph $G = (V, E)$ , an edge dominating set is a subset of edges $\subseteq E$ such that every edge in $E$ is either in $S$ or shares at least one endpoint with an edge in $S$ . Formally, for every edge $\in E$ , either $\in S$ , or there exists an edge $\in S$ such that $(u, v)$ and $(x, y)$ are adjacent (i.e., they share a common vertex). The goal of the Edge Dominating Set Problem is to find an edge dominating set $S$ of minimum size. This problem is NP-hard, and the find_edge_dominating algorithm provides an approximate solution by transforming the problem into a dominating set problem on a line graph.

Input: An undirected graph $G = (V, E)$ , represented as a NetworkX graph.
Output: A subset $\subseteq E$ such that every edge in $E$ is either in $S$ or adjacent to an edge in $S$ , with $∣ S ∣$ as small as possible.

Algorithm Overview: `find_edge_dominating`

The find_edge_dominating(graph) algorithm computes an approximate minimum edge dominating set by transforming the edge dominating set problem into a dominating set problem on the line graph of each connected component of the input graph.

Consider the algorithm implemented in Python:

import networkx as nx
import baldor.algorithm as alg

def find_edge_dominating(graph):
    """
    Compute an approximate minimum edge dominating set set for an undirected graph by transforming it into a chordal graph.

    Args:
        graph (nx.Graph): A NetworkX Graph object representing the input graph.

    Returns:
        set: A set of vertex indices representing the minimum edge dominating set set.
             Returns an empty set if the graph is empty or has no edges.
    """
    # Check if the input graph is a valid undirected NetworkX Graph; raises an error if not.
    if not isinstance(graph, nx.Graph):
        raise ValueError("Input must be an undirected NetworkX Graph.")

    # Handle edge cases: return an empty set if the graph has no nodes or no edges, as no edge dominating set is needed.
    if graph.number_of_nodes() == 0 or graph.number_of_edges() == 0:
        return set()

    # Remove all self-loop edges since they cannot be part of an edge dominating set.
    graph.remove_edges_from(list(nx.selfloop_edges(graph)))
    # Remove isolated nodes from the graph to process the remaining components, as they do not contribute to an edge dominating set.
    graph.remove_nodes_from(list(nx.isolates(graph)))

    # After removing isolated nodes, if the graph is empty, return an empty set (no edge dominating set needed).
    if graph.number_of_nodes() == 0:
        return set()

    # Initialize an empty set to store the approximate edge dominating set.
    approximate_edge_dominating = set()

    # Iterate over each connected component of the graph to compute the edge dominating set independently.
    for component in nx.connected_components(graph):
        # Extract the subgraph corresponding to the current connected component.
        subgraph = graph.subgraph(component)

        # Handle small components: if the subgraph has 2 or fewer edges, select one edge to dominate all edges in the component.
        if subgraph.number_of_edges() <= 2:
            # Add the first edge from the subgraph to the edge dominating set and move to the next component.
            approximate_edge_dominating.add(next(iter(set(subgraph.edges()))))
            continue    

        # Transform the subgraph into a line graph, where nodes represent edges of the subgraph, and edges represent adjacency between edges.
        line_graph = nx.line_graph(subgraph)    

        # Use Baldor's 2-approximation algorithm to find a dominating set in the line graph.
        # This dominating set corresponds to an edge dominating set in the original graph via the transformation.
        edge_dominating = alg.find_dominating_set(line_graph)

        # Add the edges from the dominating set (representing edges in the original subgraph) to the approximate edge dominating set.
        approximate_edge_dominating.update(edge_dominating)

    # Return the computed approximate edge dominating set set.
    return approximate_edge_dominating

Here's the step-by-step breakdown:

Input Validation and Preprocessing:
- Validates that the input is an undirected NetworkX graph.
- Returns an empty set if the graph has no nodes or edges (no edge dominating set needed).
- Removes self-loops (as they cannot be part of an edge dominating set) and isolated nodes (as they do not contribute to edge domination).
Component-wise Processing:
- Decomposes the graph into its connected components.
- For each connected component:
- Extracts the subgraph corresponding to the component.
- If the subgraph has 2 or fewer edges, selects one edge to dominate all edges in the component.
- Otherwise, proceeds with the transformation to a line graph.
Transformation to Line Graph:
- Constructs the line graph $L (G)$ of the subgraph, where:
- Each node in $L (G)$ represents an edge in the subgraph.
- Two nodes in $L (G)$ are connected if their corresponding edges in the subgraph share a common vertex.
- In $L (G)$ , a dominating set corresponds to an edge dominating set in the original subgraph: selecting a node in $L (G)$ (an edge in the subgraph) ensures that all adjacent nodes (adjacent edges) are dominated.
Dominating Set Computation:
- Uses alg.find_dominating_set (Baldor's 2-approximation algorithm) to compute a dominating set in $L (G)$ . The alg.find_dominating_set algorithm is detailed in the article Bipartite-Based 2-Approximation for Dominating Sets in General Graphs.
- The resulting dominating set in $L (G)$ is a set of edges in the original subgraph that forms an edge dominating set for that component.
Aggregation:
- Combines the edge dominating sets from all components into the final approximate edge dominating set $S$ .
- Returns $S$ .

Running Time Analysis

Let $n = ∣ V ∣$ (number of vertices) and $m = ∣ E ∣$ (number of edges) in the input graph $G$ .

Preprocessing:
- Input validation, self-loop removal, and isolated node removal: $O (n + m)$ using NetworkX operations.
Component Decomposition:
- Finding connected components: $O (n + m)$ using a depth-first search (DFS) or breadth-first search (BFS) in NetworkX.
Per Component:
- Subgraph Extraction: $O(n_c + m_c)$ , where $n_c$ and $m_c$ are the number of vertices and edges in the component. Across all components, this sums to $O (n + m)$ .
- Small Components ( $mc≤2m_c \leq 2$ ): Selecting one edge takes $O (1)$ , negligible cost.
- Line Graph Construction:
- Vertices in $L (G)$ : $m_c$ .
- Edges in $L (G)$ : Each edge in the subgraph corresponds to a vertex in $L (G)$ , and two vertices in $L (G)$ are adjacent if their corresponding edges share a vertex. For a vertex $v$ of degree $d (v)$ , its incident edges form a clique of size $d (v)$ in $L (G)$ , contributing $(d(v)2)\binom{d(v)}{2}$ edges. Total edges in $L (G)$ : $∑v∈V(d(v)2)=∑v∈Vd(v)(d(v)−1)2\sum_{v \in V} \binom{d(v)}{2} = \sum_{v \in V} \frac{d(v)(d(v)-1)}{2}$ , which is $O(∑d(v)2)O(\sum d(v)^2)$ . For sparse graphs ( $\approx n$ ), this is typically $O (m)$ , but in dense graphs, it can be $O(n^2)$ .
- Construction time: $O(mc+∑d(v)2)O(m_c + \sum d(v)^2)$ , summing to $\sum d(v)^2)$ over all components.
- Dominating Set Computation:
- alg.find_dominating_set has a runtime of $O(nL⋅log⁡nL+mL)O(n_L \cdot \log n_L + m_L)$ , where $n_L = m_c$ (vertices in $L (G)$ ) and $mL=O(∑d(v)2)m_L = O(\sum d(v)^2)$ (edges in $L (G)$ ).
- Per component: $O(mc⋅log⁡mc+∑d(v)2)O(m_c \cdot \log m_c + \sum d(v)^2)$ .
- Across all components: $O(∑(mc⋅log⁡mc+∑d(v)2))=O(m⋅log⁡m+∑d(v)2)O(\sum (m_c \cdot \log m_c + \sum d(v)^2)) = O(m \cdot \log m + \sum d(v)^2)$ .
Total Runtime:
- Combining all steps: $\cdot \log m + \sum d(v)^2)$ .
- For sparse graphs ( $\approx n$ , degrees are small), $∑d(v)2≈O(m)\sum d(v)^2 \approx O(m)$ , so the runtime simplifies to $\cdot \log m)$ .
- For dense graphs ( $\approx n^2$ ), $∑d(v)2≈O(n3)\sum d(v)^2 \approx O(n^3)$ , making the runtime $O(n^3)$ .

Approximation Factor

Transformation Property: An edge dominating set in $G$ corresponds to a dominating set in $L (G)$ . If $D$ is a dominating set in $L (G)$ , the corresponding set of edges in $G$ is an edge dominating set.
Baldor's Dominating Set Approximation: alg.find_dominating_set guarantees a 2-approximation for the dominating set problem in $L (G)$ . For a deep dive into this algorithm, check out the article Bipartite-Based 2-Approximation for Dominating Sets in General Graphs, which provides a thorough explanation.
Edge Dominating Set Approximation: Since the transformation preserves the approximation ratio, the edge dominating set computed has an approximation ratio of 2. That is, the size of the edge dominating set $\leq 2 \cdot |S^|$ , where $ParseError: KaTeX parse error: Expected group after '^' at position 2: S^̲$ is the optimal edge dominating set.
Potential Improvement: As noted in the conclusion, if alg.find_dominating_set achieves an approximation ratio $α<2\alpha < 2$ in practice, the edge dominating set approximation ratio also reduces to $α<2\alpha < 2$ , often making the solution closer to optimal.

Why This Algorithm is Better for Sparse Graphs

The find_edge_dominating algorithm is particularly efficient for sparse graphs ( $\approx n$ ) due to the following reasons:

Line Graph Size:
- In a sparse graph, the degrees $d (v)$ are small (e.g., constant or $O(log⁡n)O(\log n)$ ). Thus, the number of edges in the line graph $L (G)$ , given by $∑(d(v)2)\sum \binom{d(v)}{2}$ , is $O (m)$ . For example, if $\leq c$ (a constant), then $∑d(v)2≤c2⋅n\sum d(v)^2 \leq c^2 \cdot n$ , and since $\approx n$ , this is $O (m)$ .
- In contrast, for dense graphs ( $\approx n^2$ ), degrees are $O (n)$ , so $∑d(v)2≈O(n3)\sum d(v)^2 \approx O(n^3)$ , leading to a much larger line graph with $O(n^3)$ edges, significantly increasing the runtime.
Dominating Set Computation:
- The runtime of alg.find_dominating_set on $L (G)$ is $O(mc⋅log⁡mc+∑d(v)2)O(m_c \cdot \log m_c + \sum d(v)^2)$ . For sparse graphs, $mc≈ncm_c \approx n_c$ , and $∑d(v)2≈O(m)\sum d(v)^2 \approx O(m)$ , so this becomes $\cdot \log m)$ , which is manageable.
- In dense graphs, $∑d(v)2≈O(n3)\sum d(v)^2 \approx O(n^3)$ , making the runtime $O(n^3)$ , which is much slower.
Overall Runtime:
- For sparse graphs, the total runtime simplifies to $\cdot \log m)$ , which is nearly linear in the size of the graph, making the algorithm efficient.
- For dense graphs, the runtime becomes $O(n^3)$ , which is impractical for large graphs.
Practical Performance:
- Sparse graphs (e.g., social networks, road networks) are common in real-world applications. The algorithm's near-linear runtime in such cases makes it practical for large-scale problems, while its approximation ratio of 2 (or better if $α<2\alpha < 2$ ) ensures good solution quality.

Thus, the algorithm's design, particularly the line graph transformation and the use of alg.find_dominating_set, makes it well-suited for sparse graphs, where the computational overhead of constructing and processing the line graph remains low, and the overall runtime scales efficiently. This implementation is publicly accessible through the Python Package Index (PyPI): https://pypi.org/project/loynaz/.