![Tariffs Threaten Apple's $999 iPhone Price Point in the U.S. [Gurman]](https://www.iclarified.com/images/news/96943/96943/96943-640.jpg)
![iPhone 17 Pro Won't Feature Two-Toned Back [Gurman]](https://www.iclarified.com/images/news/96944/96944/96944-640.jpg)
![New Apple iPad mini 7 On Sale for $399! [Lowest Price Ever]](https://www.iclarified.com/images/news/96096/96096/96096-640.jpg)
 (1).webp?#)
_Christophe_Coat_Alamy.jpg?#)
![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)
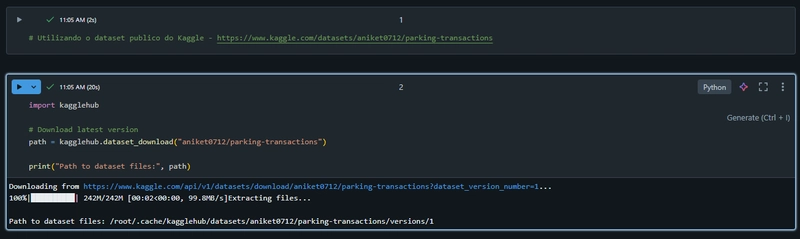
![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)
![[DEALS] The Premium Learn to Code Certification Bundle (97% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg){kind=logo}
.jpg?#)
.png?#)
Floating Point Numbers and Scientific Notation
One of the most powerful ways to represent numbers is through Scientific Notation. This system is especially useful for handling very large or very small numbers, making it ideal for computer science, where precise storage within limited memory is essential. Let’s break it down using the number 128 as an example: 1. How Do Floating-Point Numbers Work? Floating-point numbers are typically divided into two main parts: ✅ Mantissa (or significand): This represents the actual number, usually between 1 and 10. ✅ Exponent: This indicates how many times the decimal point needs to be shifted to the left or right. For example, the number 128 can be written as: 128 = 1.28 × 10² ✔ 1.28 is the mantissa ✔ 10² (i.e., 10 raised to the power of 2) is the exponent 2. How Is This Equal to 128? We know that: 10² = 100 So, 1.28 × 100 = 128 3. Why Is This Method Important?
One of the most powerful ways to represent numbers is through Scientific Notation. This system is especially useful for handling very large or very small numbers, making it ideal for computer science, where precise storage within limited memory is essential.
Let’s break it down using the number 128 as an example:
1. How Do Floating-Point Numbers Work?
Floating-point numbers are typically divided into two main parts:
✅ Mantissa (or significand): This represents the actual number, usually between 1 and 10.
✅ Exponent: This indicates how many times the decimal point needs to be shifted to the left or right.
For example, the number 128 can be written as:
128 = 1.28 × 10²
✔ 1.28 is the mantissa
✔ 10² (i.e., 10 raised to the power of 2) is the exponent
2. How Is This Equal to 128?
We know that:
10² = 100
So,
1.28 × 100 = 128
3. Why Is This Method Important?
