The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems". Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerg...

Apr 3, 2025 - 03:51

The Cryptography Handbook: Exploring RSA PKCSv1.5, OAEP, and PSS

The RSA algorithm was introduced in 1978 in the seminal paper, "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems". Over the decades, as RSA became integral to secure communications, various vulnerabilities and attacks have emerged, underscoring the importance of understanding and implementing RSA correctly.

This handbook will help you understand the internal workings of the RSA algorithm, how they have evolved over the years, and the schemes defined under various RFCs. This knowledge will help you make informed choices about the most suitable RSA schemes depending on your business requirements.

In this handbook, we’ll begin by exploring the foundational principles of the RSA algorithm. By examining its mathematical underpinnings and historical evolution, you will gain insight into the diverse array of attacks that have emerged over the years.

The narrative unfolds as an evolutionary journey: from the original, straightforward (textbook) RSA implementation, through the discovery of vulnerabilities, to the development of effective countermeasures, and further refinements as new challenges were encountered. This progression illuminates how RSA has transformed over time and also demonstrates how modern cryptographic libraries have integrated these advancements to achieve secure implementations in today’s applications.

You can also watch the associated video here:

Prerequisites

Linear Algebra: A foundational understanding of Linear Algebra and Modular Arithmetic will help you understand certain sections of the handbook, though it is not an absolute requirement. This handbook provides comprehensive explanations of mathematical expressions and their underlying concepts as they arise.

For a concise and relevant introduction to the Chinese Remainder Theorem (CRT) in the context of the handbook, you may find this resource helpful: CRT, RSA, and Low Exponent Attacks | YouTube.

Patience (and a Sense of Adventure): RFCs can sometimes get dull to read, and research papers can feel intimidating at first glance. This handbook is designed to make standard cryptographic concepts accessible to everyone, guiding you through each step with clarity and intuition. Every concept is reinforced with clear, step-by-step examples, ensuring not only a thorough understanding but also familiarity with widely used standard notations. So take your time, take a deep breath, and embrace the journey.

For visual learners, the associated video may offer a more engaging experience.

The Alice-Bob Paradigm

Throughout this handbook, you will come across numerous sequence diagrams and mathematical proofs that use the Alice-Bob Paradigm.

The Alice-Bob paradigm is a common convention in cryptography where two generic entities, often named Alice and Bob, are used to illustrate various scenarios, protocols, or cryptographic principles.

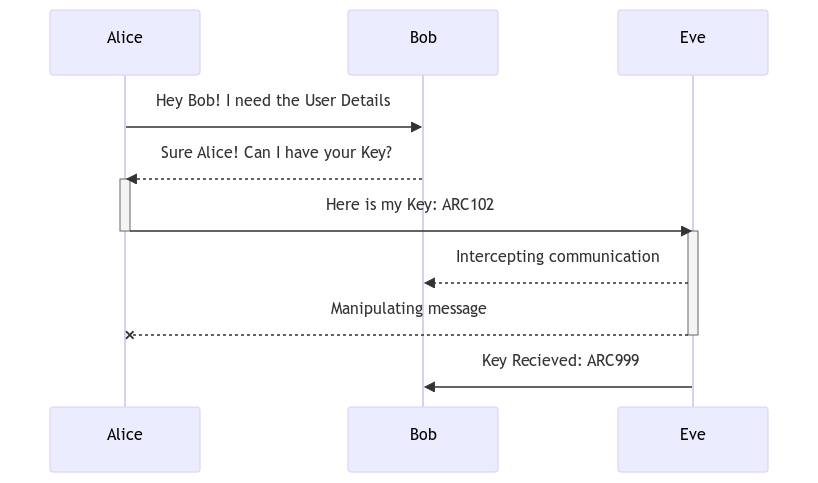
The Alice Bob Paradigm

These characters represent two parties engaged in communication, with Alice typically representing the sender or initiator, and Bob representing the receiver or responder.

We often introduce Eve as a third party, symbolizing an eavesdropper or potential attacker, adding an element of security risk, and illustrating scenarios where external entities might attempt to intercept or manipulate the communication.

The Birth of the RSA Cryptosystem

The year 1978 witnessed the birth of a new era in cryptography with the introduction of the RSA cryptosystem, named after its inventors (Rivest, Shamir, and Adleman).

This development, introduced in the paper "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems", provided a method for secure digital communication and laid the foundation for modern public-key cryptography.

At the heart of RSA lies elementary number theory – specifically, the properties of prime numbers and modular arithmetic. Let’s first understand how these key concepts form its mathematical foundations.

Prime Numbers and Composite Moduli

The algorithm starts by selecting two large prime numbers, denoted as p and q. Their product ($n = p \times q$) forms the modulus for both the public and private keys.

The security of RSA depends heavily on the fact that, while multiplying these primes is computationally straightforward, factoring the resulting large composite number n is considered infeasible for sufficiently large primes.

At this point, it’s important to note that p and q must be large prime numbers to ensure RSA’s security. Fortunately, modern libraries handle this automatically by using well-established prime-generation algorithms. As a result, you can focus on higher-level aspects of your applications without having to manage the low-level details of prime selection.

For instance, let’s have a look at OpenSSL’s RSA key generation routine which performs several checks to ensure that the resulting modulus $n = p \times q $ meets the desired bit-length requirements:

The below snippet right-shifts the product of the generated primes (stored in r1) by bitse - 4 bits to isolate the top 4 bits, which are then checked to ensure that the modulus meets the desired size criteria.

if (!BN_rshift(r2, r1, bitse - 4))
    goto err;
bitst = BN_get_word(r2);

The extracted bits (bitst) are then compared against a predefined range (from 0x9 to 0xF). This range ensures that the most significant byte of the modulus isn’t too small or too large.

if (bitst < 0x9 || bitst > 0xF) {
    bitse -= bitsr[i];

If the significant bits do not fall within the desired range, the bit length is adjusted and the prime-generation process is retried. If the number of retries exceeds a set limit, the entire process is restarted.

if (!BN_GENCB_call(cb, 2, n++))
    goto err;
if (primes > 4) {
    if (bitst < 0x9)
        adj++;
    else
        adj--;
} else if (retries == 4) {
    i = -1;
    bitse = 0;
    sk_BIGNUM_pop_free(factors, BN_clear_free);
    factors = sk_BIGNUM_new_null();
    if (factors == NULL)
        goto err;
    continue;
}
retries++;
goto redo;

To ensure that the numbers are necessarily primes, these libraries use a combination of probabilistic tests, including the Rabin-Miler Primality Testing, and sieving methods to quickly eliminate non-prime candidates.

The Euler Totient Function

For a number n that is the product of two primes, the Euler totient function is given by:

$$\varphi(n) = (p-1)(q-1)$$

This function counts the number of integers less than $n$ that are co-prime to $n$. Euler’s theorem, which states that for any integer a co-prime to n, $ a^{\varphi(n)} \equiv 1 \pmod{n}$ plays a central role in proving why RSA’s operations are reversible.

But most modern RSA cryptosystems use the Carmichael function instead of the Euler’s Totient Function. We will examine the reasoning behind this shift in the next few sections.

Computing the Keys

Now we select an integer $e$ such that $1 < e < \varphi(n)$and $\gcd(e, \varphi(n)) = 1$. This $e$ becomes the public exponent you see as a parameter in the RSA function calls you make.

With that done, now let’s determine $d$ as the modular multiplicative inverse of $e \, \, modulo \, \varphi(n)$. In other words, $d$ is computed such that:

$$e \times d \equiv 1 \pmod{\varphi(n)}$$

This step is the mathematical linchpin ensuring that decryption is the inverse operation of encryption.

In the 1978 paper, the authors explicitly provided these formulas and steps. They showed that if you encrypt a message m using $c = m^e \mod n$ and then decrypt using $m = c^d \mod n $ , the original message is recovered – thanks to the properties of modular exponentiation and Euler’s theorem. This mathematical framework was novel at the time and immediately set the stage for a new era in cryptography.

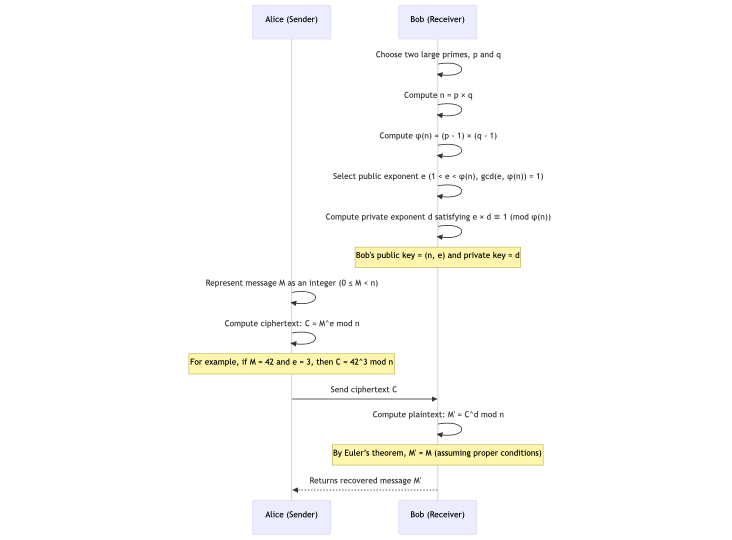
RSA Operations

Now that the mathematical foundations are laid, the RSA algorithm can be seen as a set of three core operations: Encryption, Decryption, and Signing. Throughout this handbook's next sections, we will critically analyze these operations and learn about several pitfalls in each. Then we will examine how these were averted with the birth of new schemes, each to solve a new issue discovered on the way.

Encryption

With the public key $(n, e)$ available to everyone, any user can encrypt a message $m$ (where $m$ is first encoded as an integer in the range $0 \leq m < n$ ) using the formula:

$$c = m^e \mod n$$

Here, c is the ciphertext. Because the operation is based on modular exponentiation, even if m is known, recovering m from c without knowing d is computationally hard.

Decryption

The intended recipient, who possesses the private key $d$, decrypts the cipher text $c$ by computing:

$$m = c^d \bmod n$$

Using the relationship ($e \times d \equiv 1 \pmod{\varphi(n)}$) and properties from Euler’s theorem, the above operation exactly inverts the encryption step, recovering the original message $m$.

This ensures that only the holder of the private key can read the encrypted message. This is the backbone of RSA’s use in secure communication.

The sequence diagram below wraps up our discussion so far:

Sequence Diagram: Textbook RSA Encryption

Digital Signatures

Digital signatures fulfill a different security goal: authenticity and integrity rather than confidentiality. While encryption and decryption use the public key for “locking” and the private key for “unlocking,” digital signatures reverse these roles.

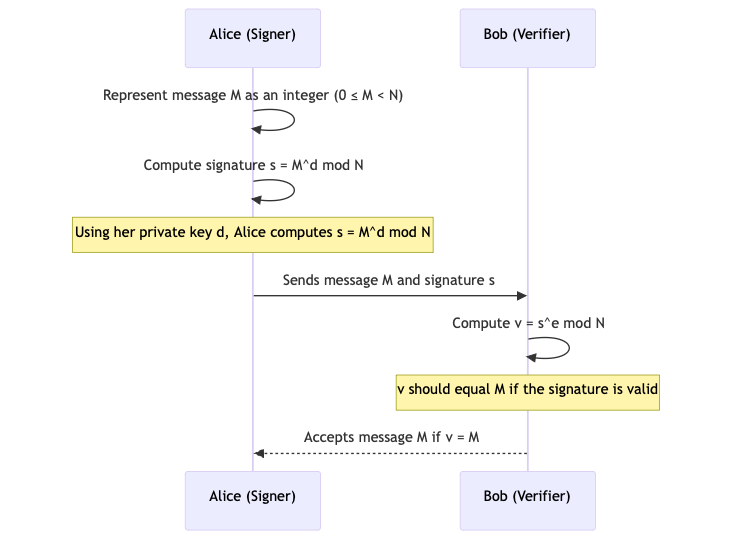
1. Signing

The author of a message uses their private key $d$ to compute a signature $s$ on the message $m$, guided by the formula mentioned below:

$$s = m^d \bmod n$$

This can later be verified by others using the corresponding public key. The purpose here is not to recover a secret message but to create a proof of authenticity.

2. Verification:

Anyone with the public key $(n, e)$ can verify that the signature s indeed belongs to the message $m$ by computing:

$$m \equiv s^e \bmod n$$

If the equivalence holds, it confirms two key points: That the message has not been tampered with (that is, integrity), and that the signature must have been generated using the private key d (that is, authenticity).
As long as $d$ is kept secret, only the legitimate signer can produce a valid signature. Take at look at the sequence diagram below to understand the complete process.

Sequence Diagram: Textbook RSA Signatures

Issues with Euler’s Totient Function in RSA

While using Euler’s Totient Function works well in theory, implementers of the scheme realized its practical downsides. Simply put, the primary issue was that Euler’s Totient Function can lead to a larger private exponent $d$ than what was necessary.

To completely appreciate this fact, let’s take a step back to understand why the size of the private exponent $d$ matters in RSA.

RSA decryption (or signing) involves computing $m^d ~~mod ~n$ which is done via modular exponentiation. The time complexity of exponentiation algorithms (like square-and-multiply) grows with the number of bits in $d$. A larger $d$ means more multiplications and squarings, that is slower decryption.

In practice, if using the Euler’s Totient Function makes $d$ roughly twice as large as what is required, then decryption can be almost twice as slow compared to using the minimal $d$. This inefficiency is especially noticeable when $e$ is small (common public exponents like 3 or 65537). A small $e$ leads to a very large $d$ under $φ(n)$.

Beyond performance, having an unnecessarily large $d$ can increase storage size slightly (a few more bytes for the key). This can also lead to interoperability quirks, which is why standards and protocols such as FIPS 186-4 [1] and RFC 8017 [2] expect $d$ to be below a certain size. We will take a detailed look at this in the next section.

To combat these issues, cryptographers utilized the Carmichael function to generate RSA keys. Before we dive into how the Carmichael function helps our case, let’s quickly understand what the Carmichael function actually is.

The Carmichael Function

The Carmichael Function, represented by $λ(n)$, also known as the reduced totient or least universal exponent, is defined as the smallest positive integer $m$ such that for every integer $a$ co-prime to $n$, $ a^m ≡ 1 (mod n)$.

To put this in easy terms, $λ(n)$ is the exponent of the multiplicative group modulo $n$ (the least common multiple of the orders of all elements). For RSA-style moduli (product of primes), the Carmichael function is guided by the formula:

$$\lambda(n) = \operatorname{lcm}(p-1,\,q-1)$$

where $n = p . q$ with $p$ and $q$ being the large primes.

You may now understand the Carmichael function better if we put it in the following way: $λ(n)$ is the least common multiple of $λ(n)$ of each prime power dividing n. So for a prime $p$, $λ(p) = φ(p) = p – 1$, and for two primes, we take the $lcm$ of $p-1 $ and $q-1.$

Mathematical Implication of The Carmichael function

The Carmichael function $λ(n)$ is a “tighter” bound. What this means is that $λ(n)$ divides $φ(n)$ (since the exponent of a finite group always divides the group order by Lagrange’s Theorem [3])

If $p$ and $q$ are both odd primes, then $p–1$ and $q–1 $ are even, so their least common multiple is roughly half of $(p–1)(q–1)$. Mathematically:

$$λ(n) = \dfrac{(p–1)(q–1)} {gcd(p–1, q–1)}$$

We can observe that this $λ(n)$ is lesser than or equal to $φ(n)$ and often considerably smaller. This means $λ(n)$ provides the minimal exponent needed for RSA’s correctness, whereas $φ(n)$might be a larger number that still works but isn’t necessary.

When you choose two large random primes $p$ and $q$, you have:

$$\varphi(n) = (p-1)(q-1) \approx n,$$

because for large primes, the subtracted ones make only a small difference compared to $p$ and $q$ themselves.

Now, since both $p-1$ and $q-1 $ are even, they each have a factor of 2. If those are their only common factors (which is often the case for random primes), then:

$$\lambda(n) = \mathrm{lcm}(p-1, q-1) \approx \frac{\varphi(n)}{2}.$$

When you compute the private exponent $d$ as the modular inverse of $e$ (a small number) modulo $ \varphi(n)$ versus modulo $\lambda(n)$, the range from which $d$ is chosen is roughly twice as large in the former case. That means the typical $d$ when computed modulo $\varphi(n)$ can be about twice as large as when computed modulo $\lambda(n)$. A larger $d$ means that during decryption (or signing) the modular exponentiation $c^d \mod n$ takes slightly more time.

Intuitively, using $λ(n)$ ensures we don’t “overshoot” the exponent required for the modular arithmetic to cycle back to 1.

A smaller $d$ makes every RSA decryption and signature operation faster. For instance, if $λ(n)$ is roughly half of $φ(n)$, then $d$ will have one less bit than it would otherwise, cutting the exponentiation work by about 50%. This is a free performance gain, as we aren’t changing the security assumptions or the key size $n$, just using the mathematically tight value for the exponent. The RSA algorithm’s security is not weakened by this and now the $d$ is different but functionally equivalent.

The Carmichael Function in Modern Implementations

The critical property for RSA ($e·d ≡ 1 ~mod ~~λ(n)$) is both necessary and sufficient for correct decryption, thanks to Carmichael’s theorem. So there’s no need for $d$ to also satisfy the stronger condition modulo $φ(n)$.

By switching to computing $d ~ modulo ~~ λ(n)$ (i.e., $d = e^{-1} ~mod ~~λ(n)$), we directly get the smallest working private exponent. Ronald Rivest himself noted this optimization in his 1999 seminal paper [4], stating that solving for $d$ using $ λ(n)$ instead of $φ(n)$ is slightly preferable because it can result in a smaller value for d.

Over time, the use of $ λ(n)$ in RSA moved from an academic suggestion to an industry standard. Today’s cryptographic standards explicitly acknowledge or require the $λ(n)$ approach.

For example, the official RSA standard (PKCS #1 v2.2, RFC 8017 [2]) defines the RSA key generation in terms of $λ(n)$. It specifies that the private exponent $d$ is chosen such that $e·d ≡ 1 (mod λ(n))$ (with $λ(n) = lcm(p–1, q–1)$). In other words, PKCS #1 expects the Carmichael function to be used for the modulus of the exponent. Likewise, NIST’s FIPS 186-4 (Digital Signature Standard) mandates that $d$ be less than $λ(n)$.

Any RSA key where $d$ is larger than $λ(n)$ is considered non-compliant in those strict contexts. This effectively forces implementations to use the smaller $λ(n)$-based exponent, since any “oversized” $d$ can be reduced $mod ~~λ(n)$ to meet the criterion.

Standards such as FIPS 186-4 [1] (the Digital Signature Standard) and RFC 8017 [2] (which specifies PKCS#1 v2.2 for RSA Cryptography) include requirements or recommendations that imply the private exponent $d$ should be as small as possible and ideally less than $ \lambda(n)$. Using $\lambda(n)$ (the least common multiple of $p-1$ and $q-1$) directly produces the smallest valid $d$, whereas using $\varphi(n)$ often results in a $d$ that is larger than necessary. This not only improves performance (by reducing the number of modular multiplications needed during decryption/signing) but also helps maintain interoperability with protocols that expect d to be below a certain size.

The Python cryptography library (PyCA cryptography) explicitly documents [5] that it uses Carmichael’s totient to generate the “smallest working value of $d$,” noting that older implementations (including the original RSA paper) used Euler’s totient and ended up with larger exponents. OpenSSL also uses the Carmichael function in their low-level RSA APIs [6].

This shift to the Carmichael function ensures that under the hood your RSA key is a bit more efficient than the ones from the late 1970s while providing the same level of security.

Issues with Raw RSA

Raw or “Textbook” RSA soon turned out to be insecure when two major weaknesses were discovered.

The operations involved in RSA are entirely deterministic, which means that for a given plaintext $m$, encryption always produces the same cipher text $C = m^e \mod n$.

An eavesdropper or an attacker, say Eve, can guess or derive plain texts by exploiting the predictability of outputs. Since RSA encryption is a public operation, an attacker can encrypt likely messages and compare results to a target cipher text – a trivial chosen plaintext attack.

Besides this, textbook RSA is also malleable. This means that its algebraic structure allows attackers to manipulate cipher texts in meaningful ways. For instance, given a cipher text $C = RSA(M)$, an attacker can multiply it by the encryption of a known value (say, r) to produce a new cipher text $C’ = C · r^e ~~mod ~n$, which decrypts to the plaintext $M·r$. When the legitimate receiver decrypts $C'$, the result is $M·r$, from which the attacker can often recover $M$.

Let’s understand these vulnerabilities with a small practical example.

Exploiting Textbook RSA’s Determinism and Malleability

Key Generation (Setup)

For our toy example, we’ll choose small prime numbers and generate an RSA key pair:

Let’s select the values of $p =3$ and $q=11$. Both of these values are prime. Now, compute the modulus and Totient Function as follows:

$$\begin{gather} \begin{split} n = p × q = 3 × 11 = 33 \\ φ(n) = (p – 1) × (q – 1) = 2 × 10 = 20 \end{split} \end{gather}$$

Now choose the public exponent. Let’s consider $e=3$ since it is coprime with $ φ(n) = 20$, and $gcd(3, 20) = 1$.

Now let’s compute the private exponent. We know that d is the modular inverse of $e ~~mod ~φ(n)$. We need to find d such that $(d × e) ≡ 1~~ (mod ~20)$. Using this knowledge we can compute $d = 7$ as $3 × 7 = 21 ≡ 1 ~~ (mod~ 20)$.

Finally, the public key is $(n = 33, ~ e = 3)$ and the private key (secret) is $d = 7$.

Encryption Process

Now, let’s encrypt a simple message using the above key. Let us select our plaintext to be $M = 4$. The cipher text in this case would be:

$$\begin{gather} \begin{split} C = 4^3 ~~mod ~33 \\ C = 64 ~~mod ~33 \\ C = 64 – 33×1 = 31 \end{split} \end{gather}$$

To consolidate the findings so far, if we encrypt message $4$ with the public key $(e=3, n=33)$, we will produce the cipher text $31$. Now, let’s try the exploits.

Determinism Exploit (Ciphertext Guessing Attack)

Textbook RSA is deterministic – the same plaintext always yields the same ciphertext (with no randomness involved). An attacker who intercepts the ciphertext $C=31$ can exploit this by encrypting likely plaintext guesses and comparing results:

The adversary, say Eve, will try encrypting candidate plaintexts with the public key and see which one produces $31$. They may pick randomized values to increase their efficiency:

$$\begin{gather} \begin{aligned} Guess~ M = 1 ⇒ 1^3~~ mod ~33 = 1 \\ Guess~ M = 2 ⇒ 2^3~~ mod ~33 = 8 \\ Guess~ M = 3 ⇒ 3^3~~ mod ~33 = 27 \\ Guess~ M = 4 ⇒ 4^3~~ mod ~33 = 31 \\ \end{aligned} \end{gather}$$

By simply comparing ciphertexts, the attacker finds that encrypting $4$ yields 31, which matches the intercepted ciphertext. Thus, the attacker learns the original plaintext $M$ was $4$. This is possible because there’s no randomization in textbook RSA – an eavesdropper can identify a message by trial encryption of guesses, breaking confidentiality if the message space is small or guessable.

Malleability Exploit (Ciphertext Manipulation Attack)

Raw RSA is also malleable. This means an attacker can take a ciphertext and modify it in a way that results in a predictable change in the decrypted plaintext. Let’s understand how this works.

RSA has a multiplicative property, that is, multiplying two ciphertexts corresponds to multiplying their plaintexts before encryption:

$$E(M_1) \cdot E(M_2) \mod n = (M_1^e \mod n)\times(M_2^e \mod n) \mod n = (M_1 \cdot M_2)^e \mod n$$

The sequence diagram below explains how the malleability exploit works in naive RSA.

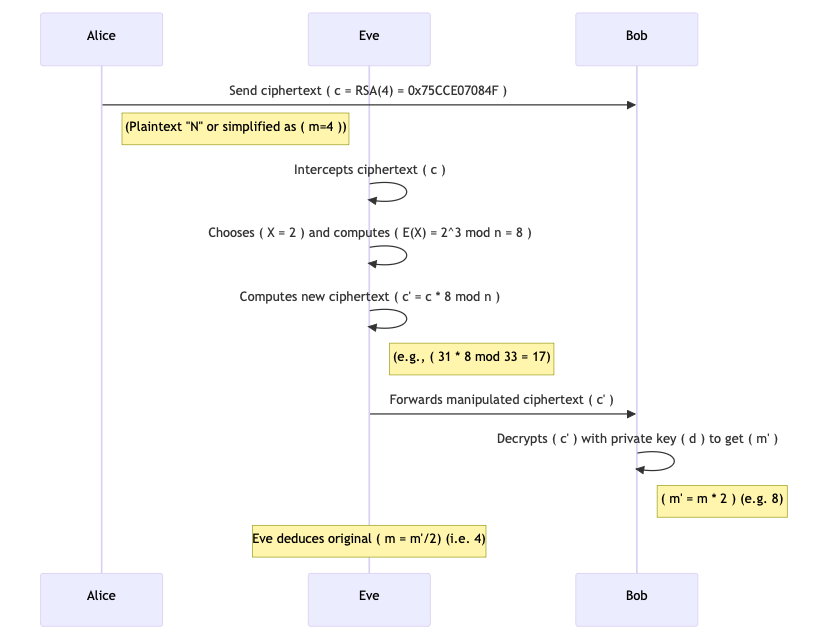
Sequence Diagram: Malleability Exploit

Alice sends a ciphertext to Bob after the initialization phase. Note that by this point, n and e are public knowledge. Eve intercepts this ciphertext by using mechanisms such as a MiTM (Man in the Middle) attack.

Now, Eve picks a known value to manipulate the message. Let’s say the attacker chooses $X = 2$ (with the intent to double the original plaintext).

Then they compute the encryption of X using the public key:

$$E(X) = 2^3 \mod 33 = 8.$$

Now, Eve multiplies the original ciphertext by this value (mod n) to get a new ciphertext:

$$\begin{gather} \begin{split} C{\prime} = C \times E(X) \mod n = 31 \times 8 \mod 33 \\ C{\prime} = 248~~ mod~ 33 = 248 – 33×7 = 248 – 231 = 17 \end{split} \end{gather}$$

This new ciphertext $C{\prime}$ is the encryption of the product of the original plaintext and $2$. If we directly encrypted $M \times X = 4 \times 2 = 8$ with RSA, we would get $8^3 \mod 33 = 512 \mod 33 = 17$. This means that $C′$ corresponds to the plaintext $8$, which is the original message $4$ multiplied by $2$.

In a real-world chosen ciphertext attack, the attacker may have access to a decryption oracle or observe a system response that reveals information about $M{\prime}$. The decryption result $8$ is exactly $M \times 2$ (the original message multiplied by the attacker’s chosen factor). Knowing the factor $X = 2$, the attacker can deduce the original message by dividing: $8/ 2 = 4$.

Note that Eve has not broken the mathematical foundations behind RSA here. They have only used the public key to compute an encryption of $2$, and then combined it with the intercepted ciphertext. They don’t know the original plaintext yet, but they have manipulated the ciphertext in a way that they know the new plaintext is twice the original message.

Low-Exponent Attacks

Beyond determinism and malleability exploits, textbook RSA is also vulnerable to Low-Exponent Attacks. Using a small public exponent like $e = 3$ (or sometimes $17$) was popular because it used to speed up encryption and signature verification. But this soon turned out to be a security concern.

When RSA uses a small public exponent (say, $e = 3$) and the plaintext is very short (so that $M^3$ is smaller than the modulus $n$), the encryption does not “wrap around” modulo $n$. Mathematically:

$$c = M^3 \mod n = M^3 \quad \text{(if $ M^3 < n $)}$$

Let’s understand this with an easy example:

Consider our plaintext to be: $M = 5$. We compute $M^3$ as $M^3 = 5^3 = 125$.

Now assume $n$ is a $4096$‑bit number which is large compared to $125$. In this case, the ciphertext is simply $c = 125$. Eve intercepting $c = 125$ can compute the cube root of $125$ to get the plaintext: $\sqrt[3]{125} = 5$ thus recovering $M$ directly.

This shows that if $M$ is small enough, the ciphertext leaks the plaintext when $e$ is low.

Håstad’s Broadcast Attack: Low Exponent Meets Multiple Recipients

In 1985, Johan Håstad’s highlighted the broadcast attack that illustrates the danger of a low exponent, $e$, when the same message is sent to multiple parties as a broadcast.

Imagine Alice wants to send the same plaintext message M to three different recipients. Each recipient has their own RSA public key with modulus $N_1, N_2, N_3,$ but for speed all use $e = 3$ (a common practice historically). Alice encrypts $M$ with each public key, yielding ciphertexts:

$$\begin{gather} \begin{split} C_1 = M^3 \bmod N_1 \\ C_2 = M^3 \bmod N_2 \\ C_3 = M^3 \bmod N_3 \end{split} \end{gather}$$

Eve, who intercepts all three $C_1, C_2, C_3$ can recover M without breaking any single RSA key.

Since each $N_i $ is different (and we assume they are pairwise coprime, as RSA keys should be), the attacker can use the Chinese Remainder Theorem (CRT) to combine the three congruences $x \equiv C_i \pmod{N_i}$. Note that at this point Eve only has $C_1$, $C_2$ and $C_3$. They do not have the plaintext $M$ or $M^3$ and yet they can reconstruct $M^3$ with the intercepted data. To understand the Chinese Remainder Theorem and this reconstruction, you may follow this: CRT, RSA, and Low Exponent Attacks | Youtube.

There is a unique solution modulo $N_1N_2N_3$ for $x$, and that solution turns out to be an integer, $x = M^3$ (because the true integer $M^3$ is smaller than the product $N_1N_2N_3$ of each $M < N_i $ ). In essence, CRT lets Eve reconstruct $M^3$ exactly. Once they have $M^3$ as an ordinary integer, they simply take the cube root to find $M$. There’s no need to factor any modulus or invert the RSA function – the math falls out due to the low exponent.

The sequence diagram below aims to provide a high-level understanding of the attack:

Sequence Diagram: Håstad’s Broadcast Attack

Now let’s see this attack in action with a sample:

Suppose three different RSA public keys all use exponent $e=3$, with moduli $ n_b = 187$ (for Bob),
$n_c = 115 $ (for Carol), and $n_d = 87$ (for Dave).

These $n_i$ are pairwise coprime ($gcd$ of each pair is $1$). Now assume the same plaintext message $M$ is encrypted with each public key. Let’s take a concrete $M$. For example with $M=42$, we will have:

$$\begin{gather} \begin{split} c_b = M^3 \bmod n_b \\ c_c = M^3 \bmod n_c \\ c_d = M^3 \bmod n_d \\ \end{split} \end{gather}$$

On calculating these, we have:

$$\begin{gather} \begin{split} c_b = 42^3 \bmod 187 = 36 \\ c_c = 42^3 \bmod 115 = 28 \\ c_d = 42^3 \bmod 87 = 51 \\ \end{split} \end{gather}$$

So the three ciphertexts observed are $36$, $28$, and $51$, respectively. Eve who knows $n_b, n_c, n_d$ and these ciphertexts can now recover $M$ as follows:

Eve will compute the total modulus $N = n_b \cdot n_c \cdot n_d = 187 \times 115 \times 87 = 1,870,935.$ (This is the modulus for the combined system of congruences).
Now Eve will compute the partial products for each congruence:

$$\begin{gather} \begin{split} N_b = \frac{N}{n_b} = \frac{1,870,935}{187} = 10,005 \\ N_c = \frac{N}{n_c} = \frac{1,870,935}{115} = 16,269 \\ N_d = \frac{N}{n_d} = \frac{1,870,935}{87} = 21,505 \end{split} \end{gather}$$

At this point, Eve needs the inverses of each $N_i$ modulo its corresponding $n_i$:
- First Eve computes $M_b = (N_b)^{-1} \bmod n_b$, i.e. the number $M_b$ such that $N_b \cdot M_b \equiv 1 \pmod{187}$. In this case, $N_b = 10005$. Using the extended Euclidean algorithm, Eve can find $M_b = 2$ (since $10005 \times 2 = 20010 \equiv 1 \pmod{187}$).
- Then Eve computes $M_c = (N_c)^{-1} \bmod n_c$. Here $N_c = 16269$. The inverse mod $115$ turns out to be $M_c = 49$ (For verification: $16269 \times 49 \equiv 1 \pmod{115}$).
- Next up, Eve computes $M_d = (N_d)^{-1} \bmod n_d$. For $N_d = 21505$, the inverse mod $87$ is $M_d = 49$ as well (coincidentally the same value in this case, since $21505 \times 49 \equiv 1 \pmod{87}$).

Now Eve reconstructs the combined value using the Chinese Remainder Theorem for three congruencies. The construction of this formula is beyond the scope of this handbook, but to completely understand how this springs into action, you may go through this video: CRT, RSA and Low Exponent Attacks | Youtube.

$$C \;=\; c_b \cdot N_b \cdot M_b \;+\; c_c \cdot N_c \cdot M_c \;+\; c_d \cdot N_d \cdot M_d \pmod{N}$$

On substituting the numbers:

$$C = 36 \cdot 10005 \cdot 2 \;+\; 28 \cdot 16269 \cdot 49 \;+\; 51 \cdot 21505 \cdot 49 \pmod{1,870,935}$$

Let’s carefully evaluate each term:

$$\begin{gather} \begin{split} 36 \cdot 10005 \cdot 2 = 720,360 \\ 28 \cdot 16269 \cdot 49 = 22,341,348 \\ 51 \cdot 21505 \cdot 49 = 5,37,40,995 \\ \end{split} \end{gather}$$

Summing these gives a raw total of $7,20,360 + 2,23,21,068 + 5,37,40,995 = 7,67,82,423$. Now reduce this modulo $N = 1,870,935$:

$$\begin{align} \begin{split} C \equiv 7,67,82,423 \pmod{1,870,935}\\ C = 74,088 \\ \end{split} \end{align}$$

Now Eve will simply take the cube root of $C: \sqrt[3]{74088} = 42$, which is the original plaintext.
Eve has successfully recovered $M$.

The key takeaway from these attacks is that without proper defenses. RSA alone does not satisfy modern definitions of security. It is not resistant to chosen-plaintext or chosen-cipher text attacks. This gap between the theoretical one-way function (RSA’s trapdoor permutation) and a secure encryption scheme became evident as implementers found that naive RSA could be “broken” by various clever tricks.

To counter these weaknesses, standards bodies introduced padding schemes to strengthen RSA encryption. In the following sections, you will learn about each of these paddings schemes and how they’ve been exploited over the years.

Introduction to Padding Schemes in RSA

Before we dive into the padding schemes and how it helps our case, let’s quickly recap the need for padding in RSA.

Textbook RSA encryption is deterministic. The same plaintext always produces the same ciphertext under a given public key. This determinism makes raw RSA insecure. An attacker can guess possible messages, encrypt them with the public key, and compare with the target ciphertext to see which guess matches.

Beyond determinism, small-exponent attacks illustrate why padding is critical. If the message $m$ is too small relative to the modulus, raising it to a small public exponent (like $e=3$) might not wrap around $N$. Padding the plaintext with random data before encryption remedies these problems by making the ciphertext unpredictable and ensuring $m^e$ spans the modulus’ range.

Public Key Cryptography Standards (PKCS#1 v1.5)

In 1998, Kaliski and RSA Laboratories introduced PKCS#1 v1.5 to the world in a public publication [7]. In PKCS#1 v1.5, every RSA‐encrypted message is wrapped inside a special “encryption block” $EB$. This block ensures that the raw message is both the right size for RSA and padded in a way that’s hard to tamper with.

In this scheme, the plaintext is padded to the size of the modulus $N$ (in bytes) as:

$$EB = 00 ~||~ BT ~||~ PS ~||~ 00 ~||~ M$$

Here, $0x00$ (Leading Zero Byte) is always at the front. It ensures that, when the concatenated string $EB$ is converted to a big‐endian integer, the value is less than the RSA modulus (that is, we don’t end up with a number too large for RSA to handle). You will better appreciate this fact when we dive into the mathematics behind this.

The next octet is the Block Type, $BT$, which tells us the “type” of padding being used. The standard defines three possible $BT$ values: $00, 01, $ and $02$- to support different operations. For example, $BT=00$ and $BT = 01$ is used for private-key operations (such as digital signatures) and $BT = 02$ is used for public-key operations. For encryption under PKCS#1 v1.5, this is always $0x02$. It’s basically a label that says, “This is an encryption block, not something else”.

The next block is the Padding String $PS$. This is a string of nonzero random bytes. This is crucial for security because it introduces randomness into each encryption. If the same message is encrypted multiple times, these random bytes ensure that each ciphertext looks different, foiling many simple attacks that rely on seeing repeated patterns.

The next octet, $0x00$, is a Delimiter. This single zero byte marks the end of the padding. During decryption, this helps the recipient quickly identify where the padding stops and the real message begins.

Finally, we have the actual data you want to protect – $M$. Once the recipient has verified the padding, they know exactly where to find this message.

This mechanism helped solve the deterministic issue of naive RSA. In the next sections, let’s understand the mathematics involved in PKCS#1 v1.5 padding and its security implications.

The Mathematics Behind PKCS#1 v1.5

Before we begin, let’s get our symbols and abbreviations correct. We will use upper-case symbols (such as $EB$) to denote octet strings and bit strings. We will use lower-case symbols (such as $n$) to denote integers.

In PKCS#1 v1.5, we will use $k$ to represents the length of the RSA modulus $n$ in bytes. For example, if you have a $1024$-bit RSA key, then the RSA modulus $n$ is a $1024$-bit number. Since there are $8$ bits in a byte, if your RSA modulus is $L$ bits long, then:

$$k = \left\lceil \frac{L}{8} \right\rceil = \frac{1024}{8} = 128 \text{ bytes}$$

The total length of the encryption block will be equal to this RSA key length $k$ (in bytes). Now here the length of the data $M$ shall not be more than $k-11$ octets, since the 11 bytes are consumed by the blocks – $0x00 ~||~ 0x02 ~||~ PS ~||~ 0x00$. This limitation guarantees that the length of the padding string $PS$ is at least eight octets, which is a security condition in PKCS#1v1.5:

$$∣PS∣=k~−∣M∣−~3$$

For example, with a $1024$-bit RSA modulus, the value of $k$ comes out to be $128$. Here Alice could encrypt up to $128 - 11 = 117$ bytes of data. The $11$ bytes are used for the $0x00 ~||~ 0x02 ~||~ PS ~||~ 0x00$ structure. The random $PS $ ensures that each encryption of the same message produces a different ciphertext, preventing the deterministic encryption problem.

RSA doesn’t directly operate on the bytes. Once the padded string $EB$ is ready, it needs to be converted into an integer guided by the Octet String to Integer Primitive (OS2IP) formula:

$$x = \sum_{i=1}^{k} 2^{8(k - i)} \,\mathrm{EB}_i$$

where $EB_i$ are the octets of $EB$ from first to last. In other words, $EB_1$ (the first byte) is the most significant byte, and $EB_k$ (the last byte) is the least significant. Now Alice can simply encrypt this block using $C = x^c \mod n$.

To solidify our learnings so far, let’s apply this to a sample plaintext and find the padded blocks.

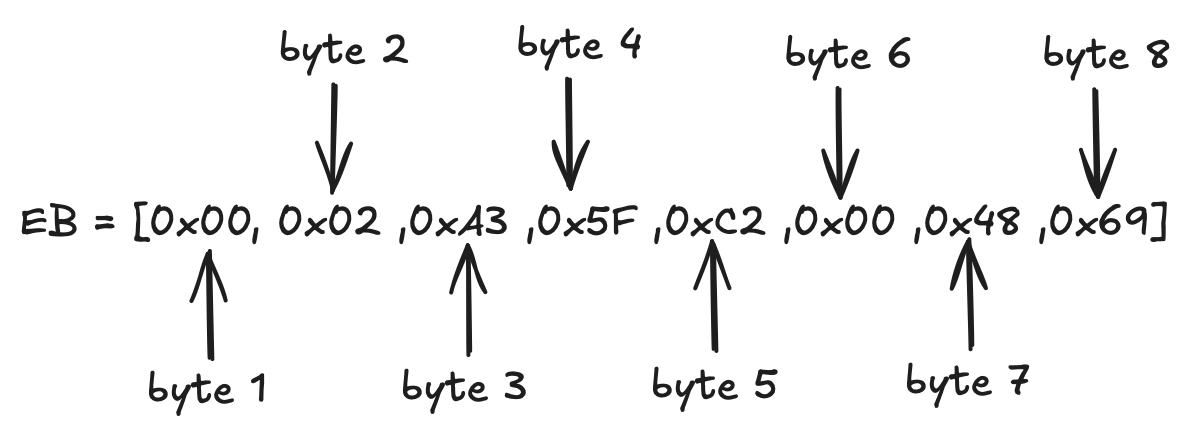
Let’s assume the RSA modulus is $8$ bytes long ($k=8$). Suppose we want to encrypt a message $M$ that is $2$ bytes long. Then the padding string $PS$ must fill the remaining space:

$$Total ~ bytes=k=8=1(0x00)+1(BT)+∣PS∣+1(delimiter)+∣M∣$$

Since $∣M∣=2$ and there are $∣M∣=2∣$ fixed bytes, can find the required length of the padding string:

$$∣PS∣=8−3−2=3 ~ bytes$$

Let’s pick 3 arbitrary nonzero bytes for $PS$, say - $0xA3, ~0x5F, ~0xC2$. And let’s say the message is the ASCII text “Hi”. In hexadecimal, that’s: $0x48$ for 'H' and $0x69$ for 'i'.

Thus, the complete encryption block becomes:

Sample Encryption Block in PKCS#1 v1.5

Now we will convert this octet string to an integer using the OS2IP formula we discussed above:

$$x = \sum_{i=1}^{k} 2^{8(k - i)} \,\mathrm{EB}_i$$

For our example, with $k=8$ the conversion is:

$$x= 0x00×256^7+0x02×256^6+0xA3×256^5+0x5F×256^4+0xC2×256^3+0x00×256^2+0x48×256^1+0x69×256^0$$

Note that the hexadecimal values can be converted to decimal as needed. For instance, $0xA3 = 163, 0x5F = 95, 0xC2 = 194, 0x48 = 72,$ and $0x69 = 105$.

There is an interesting observation in the application of this formula. Because the first two bytes are fixed ($0x00$ and $0x02$), the integer $x$ has a known lower bound. The contribution of the first two bytes is:

$$0×256^ 7 +2×256^ 6 =2×256^ 6$$

The rest of the bytes ($PS$, the delimiter, and $M$) add some value that is at least $0$ and at most just less than $256^6$ (since the second byte is fixed as $0x02$ and cannot be $0x03$). Thus, $x$ is in the range:

$$2×256 ^ 6 ≤x<3×256 ^ 6$$

This property which makes the range predictable, paved the way for the Bleichenbacher attack (also known as the “padding oracle” attack). If a system reveals whether a decrypted block is “correctly padded,” an attacker can systematically probe different ciphertexts and narrow down the plaintext – because the attacker knows it must lie in that narrow range. Let’s take a detailed look at the Bleichenbacher attack in the next sections and understand how the exploit works.

The Bleichenbacher Attack

In 1998, Daniel Bleichenbacher published a seminal paper [8] demonstrating an adaptive chosen-ciphertext attack against RSA with PKCS#1 v1.5 padding. The Bleichenbacher Attack, also dubbed as the “million messages” attack, demonstrated that if an attacker has access to an oracle that tells whether a submitted ciphertext decrypts to a properly padded plaintext (that is, whether the PKCS#1 v1.5 formatting is correct), the attacker can gradually recover the full plaintext. Let’s break down how this attack works:

First, Eve needs an Oracle. The attack assumes the attacker can query a system, such as an SSL/TLS server, and find out if a given ciphertext $C$ is PKCS#1 v1.5 conformant. In the 1998 paper, Bleichenbacher exploited the fact that a TLS server, when presented with an improperly padded RSA-encrypted premaster secret, would respond with a specific error alert if the padding was wrong. Essentially, the server acted as an oracle: it would decrypt $C$ with its private key and simply tell the attacker “padding OK” or “padding error” (the error could be timing-based or an explicit alert).

Note that the oracle does not reveal the plaintext. It only reveals a single bit of information at a time: “valid padding or not.” This might seem harmless, but Bleichenbacher showed that it’s enough to eventually recover the plaintext.

To quickly recap, the attacker’s goal is to find the unknown message integer $m$ (the PKCS#1-padded plaintext as an integer) given its ciphertext $C = m^e \bmod N$, using the oracle. We know that if $m$ is properly padded, it lies in a specific numeric range: $2B \le m < 3B$ where $B = 2^{8*(k-2)}$, as defined earlier.

If $k=128$ bytes, then $B=2^{8*126}$, and a correctly padded $m$ will start with $0x00 ~||~0x02$, so it’s between $2B$ and $3B$. The attacker, Eve, initially only knows that $m$ is in the range $[2B, 3B)$.

In the Bleichenbacher Attack, Eve will exploit RSA’s multiplicative property. They will choose a number $s$ (called the multiplier) and compute a new ciphertext $C' = (C s^e) \bmod N$. This $C'$ here corresponds to a new plaintext: $m' = m s \bmod N$ (because $C' \equiv m^e * s^e \equiv (ms)^e \pmod{N}$).

To begin the attack, Eve finds some $s_0$ such that $C_0 = C * (s_0)^e \mod N$ yields a valid padding. This is referred to as the Blinding step. This is usually easy – for example, $s_0$ can be chosen so that $m * s_0$ is just slightly above $N$, which almost certainly will wrap around and land in $[2B,3B)$. The attacker does not know $m$ to verify this directly. They rely on the padding oracle’s yes/no response to infer that the blinded plaintext $(m×s_0)\mod N$ falls in the correct range.

If the oracle returns “valid padding” for a given $ s_0$, it tells the attacker that $s_0 \mod N$lies between $2B$and $3B$. Mathematically:

$$2B≤(m×s_0)~mod N<3B$$

Now, Eve will try to try to narrow down this range in a loop, which is often referred to as the interval having step. Initially, Eve had one wide interval $[a, b] = [2B, 3B)$ that contains $m$. In each iteration, Eve tries increasing values of $s$ (starting from a certain minimum) until the oracle returns “padding OK” for $C' = C_0 * s^e$. Suppose this happens at some $s = s_i$. Given this feedback, Eve now knows:

$$2