2503. Maximum Number of Points From Grid Queries
2503. Maximum Number of Points From Grid Queries Difficulty: Hard Topics: Array, Two Pointers, Breadth-First Search, Union Find, Sorting, Heap (Priority Queue), Matrix You are given an m x n integer matrix grid and an array queries of size k. Find an array answer of size k such that for each integer queries[i] you start in the top left cell of the matrix and repeat the following process: If queries[i] is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all 4 directions: up, down, left, and right. Otherwise, you do not get any points, and you end this process. After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times. Return the resulting array answer. Example 1: Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2] Output: [5,8,1] Explanation: The diagrams above show which cells we visit to get points for each query. Example 2: Input: grid = [[5,2,1],[1,1,2]], queries = [3] Output: [0] Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3. Constraints: m == grid.length n == grid[i].length 2
2503. Maximum Number of Points From Grid Queries
Difficulty: Hard
Topics: Array, Two Pointers, Breadth-First Search, Union Find, Sorting, Heap (Priority Queue), Matrix
You are given an m x n integer matrix grid and an array queries of size k.
Find an array answer of size k such that for each integer queries[i] you start in the top left cell of the matrix and repeat the following process:
- If
queries[i]is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all4directions: up, down, left, and right. - Otherwise, you do not get any points, and you end this process.
After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.
Return the resulting array answer.
Example 1:
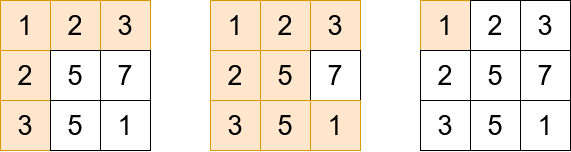
- Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
- Output: [5,8,1]
- Explanation: The diagrams above show which cells we visit to get points for each query.
Example 2:
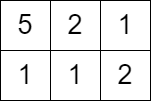
- Input: grid = [[5,2,1],[1,1,2]], queries = [3]
- Output: [0]
- Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 105k == queries.length1 <= k <= 1041 <= grid[i][j], queries[i] <= 106
Hint:
- The queries are all given to you beforehand so you can answer them in any order you want.
- Sort the queries knowing their original order to be able to build the answer array.
- Run a BFS on the graph and answer the queries in increasing order.
Solution:
We need to determine the maximum number of points we can collect starting from the top-left cell of a grid for each query. The points are earned by visiting cells with values strictly less than the query value, and movement is allowed in all four directions (up, down, left, right).
Approach
- Dijkstra's Algorithm with Priority Queue: We use a modified version of Dijkstra's algorithm to compute the minimal maximum value required to reach each cell from the top-left corner. This value represents the smallest maximum value encountered along the path from the start cell to each respective cell.
- Sorting and Binary Search: After computing the minimal maximum values for all cells, we sort these values. For each query, we use binary search to determine how many cells have a minimal maximum value less than the query value, which gives the answer for that query.
Let's implement this solution in PHP: 2503. Maximum Number of Points From Grid Queries
/**
* @param Integer[][] $grid
* @param Integer[] $queries
* @return Integer[]
*/
function maxPoints($grid, $queries) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example 1
$grid1 = [
[1, 2, 3],
[2, 5, 7],
[3, 5, 1]
];
$queries1 = [5, 6, 2];
print_r(maxPoints($grid1, $queries1)); // Output: [5, 8, 1]
// Example 2
$grid2 = [
[5, 2, 1],
[1, 1, 2]
];
$queries2 = [3];
print_r(maxPoints($grid2, $queries2)); // Output: [0]?>
Explanation:
- Dijkstra's Algorithm: We use a priority queue (min-heap) to process cells in order of their value. This ensures that we always expand the cell with the smallest maximum value encountered so far, allowing us to compute the minimal maximum value required to reach each cell.
- Binary Search for Queries: After sorting the minimal maximum values, each query is answered using binary search to efficiently count how many values are less than the query value. This count gives the maximum number of points for that query.
This approach efficiently processes the grid and queries, ensuring optimal performance even for large grids and numerous queries.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks


































































![Apple's M5 iPad Pro Enters Advanced Testing for 2025 Launch [Gurman]](https://www.iclarified.com/images/news/96865/96865/96865-640.jpg)
![M5 MacBook Pro Set for Late 2025, Major Redesign Waits Until 2026 [Gurman]](https://www.iclarified.com/images/news/96868/96868/96868-640.jpg)
![Apple to Revamp Health App with AI-Powered Doctor [Gurman]](https://www.iclarified.com/images/news/96870/96870/96870-640.jpg)














![What Google Messages features are rolling out [March 2025]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2023/12/google-messages-name-cover.png?resize=1200%2C628&quality=82&strip=all&ssl=1)































































































































































![[The AI Show Episode 141]: Road to AGI (and Beyond) #1 — The AI Timeline is Accelerating](https://www.marketingaiinstitute.com/hubfs/ep%20141.1.png)
![[The AI Show Episode 140]: New AGI Warnings, OpenAI Suggests Government Policy, Sam Altman Teases Creative Writing Model, Claude Web Search & Apple’s AI Woes](https://www.marketingaiinstitute.com/hubfs/ep%20140%20cover.png)
![[The AI Show Episode 139]: The Government Knows AGI Is Coming, Superintelligence Strategy, OpenAI’s $20,000 Per Month Agents & Top 100 Gen AI Apps](https://www.marketingaiinstitute.com/hubfs/ep%20139%20cover-2.png)

























































































































![From broke musician to working dev. How college drop-out Ryan Furrer taught himself to code [Podcast #166]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743189826063/2080cde4-6fc0-46fb-b98d-b3d59841e8c4.png?#)






![[FREE EBOOKS] The Ultimate Linux Shell Scripting Guide, Artificial Intelligence for Cybersecurity & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)
























OSAMU-NAKAMURA.jpg?width=1920&height=1920&fit=bounds&quality=80&format=jpg&auto=webp#)







.png?#)