Reduce sin(2 * pi * n)
I would like to compute an integral and evaluate it. The result has many sin and cos that have a n (integer) multiplying pi. How can I modify my code so that cos(2 * pi * n) = 1? import sympy as sp x = sp.Symbol('x') n = sp.Symbol('n', integers=True) h = sp.Symbol('h') l = sp.Symbol('l') borne_inf = 0 borne_sup = sp.Symbol('l') integrale = sp.integrate(((4*h/l**2)*x*(x-1))* sp.sin(n * sp.pi * x / l), (x, borne_inf, borne_sup))
I would like to compute an integral and evaluate it. The result has many sin and cos that have a n (integer) multiplying pi. How can I modify my code so that cos(2 * pi * n) = 1?
import sympy as sp
x = sp.Symbol('x')
n = sp.Symbol('n', integers=True)
h = sp.Symbol('h')
l = sp.Symbol('l')
borne_inf = 0
borne_sup = sp.Symbol('l')
integrale = sp.integrate(((4*h/l**2)*x*(x-1))* sp.sin(n * sp.pi * x / l), (x, borne_inf, borne_sup))





























































![Apple's M5 iPad Pro Enters Advanced Testing for 2025 Launch [Gurman]](https://www.iclarified.com/images/news/96865/96865/96865-640.jpg)
![M5 MacBook Pro Set for Late 2025, Major Redesign Waits Until 2026 [Gurman]](https://www.iclarified.com/images/news/96868/96868/96868-640.jpg)
![Apple to Revamp Health App with AI-Powered Doctor [Gurman]](https://www.iclarified.com/images/news/96870/96870/96870-640.jpg)








































































































































































![[The AI Show Episode 141]: Road to AGI (and Beyond) #1 — The AI Timeline is Accelerating](https://www.marketingaiinstitute.com/hubfs/ep%20141.1.png)
![[The AI Show Episode 140]: New AGI Warnings, OpenAI Suggests Government Policy, Sam Altman Teases Creative Writing Model, Claude Web Search & Apple’s AI Woes](https://www.marketingaiinstitute.com/hubfs/ep%20140%20cover.png)
![[The AI Show Episode 139]: The Government Knows AGI Is Coming, Superintelligence Strategy, OpenAI’s $20,000 Per Month Agents & Top 100 Gen AI Apps](https://www.marketingaiinstitute.com/hubfs/ep%20139%20cover-2.png)






















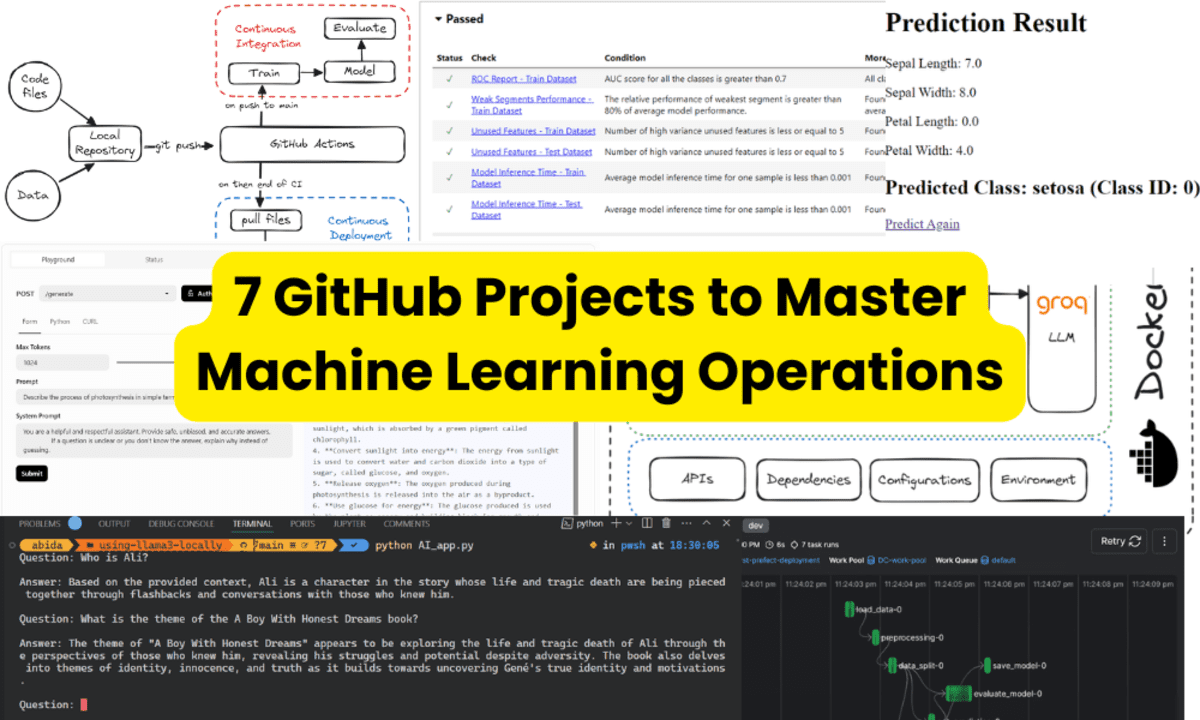




































































































![From broke musician to working dev. How college drop-out Ryan Furrer taught himself to code [Podcast #166]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743189826063/2080cde4-6fc0-46fb-b98d-b3d59841e8c4.png?#)






![[FREE EBOOKS] The Ultimate Linux Shell Scripting Guide, Artificial Intelligence for Cybersecurity & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



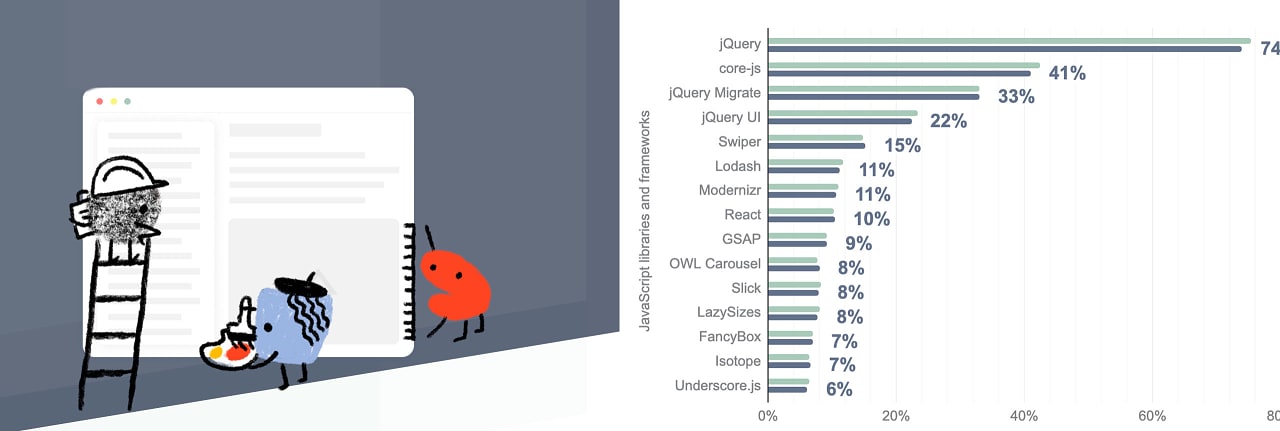

















.jpg?width=1920&height=1920&fit=bounds&quality=80&format=jpg&auto=webp#)


OSAMU-NAKAMURA.jpg?width=1920&height=1920&fit=bounds&quality=80&format=jpg&auto=webp#)






.png?#)